VLM : 논문 리뷰 : PoE-World: Compositional World Modeling with Products of Programmatic Experts

PoE-World: Compositional World Modeling with Products of Programmatic Experts 논문 학습 노트

Terminology (용어 설명)

• World Model: Agent가 환경(environment)이 어떻게 작동하는지(행동에 따라 상태가 어떻게 변하는지)를 학습한 내부 모델. 이를 통해 실제 환경에서 시행착오를 겪지 않고 시뮬레이션을 통해 계획(planning)을 세울 수 있음.
• Product of Experts (PoE): 여러 개의 단순한 확률 모델(experts)들을 곱하여 하나의 복잡한 고차원 확률 분포를 모델링하는 기법. 각 expert는 자신이 아는 특정 규칙에 대해서만 의견을 제시하고, 이를 종합하여 최종 예측을 수행함.
• Programmatic Experts: 이 논문에서 제안한 개념으로, 환경의 특정 물리 법칙이나 인과 관계(causal laws)를 설명하는 짧은 Python 코드 조각들.
• Compositional Generalization (구성적 일반화): 학습한 구성 요소(지식)들을 새로운 방식으로 재조합하여, 본 적 없는 새로운 상황이나 환경에서도 올바르게 추론하고 작동하는 능력.
• OCAtari (Object-Centric Atari): Atari 게임의 화면을 픽셀 단위가 아닌, 객체(object) 단위(예: 플레이어, 적, 열쇠 등의 위치와 속성)로 파싱 하여 제공하는 라이브러리.
• Hierarchical Planning: 계획을 세울 때, 상위 레벨(예: "열쇠를 잡으러 간다")과 하위 레벨(예: "오른쪽으로 이동, 점프")로 계층을 나누어 복잡한 문제를 해결하는 방식.

---

Purpose of the Paper

• 기존 Deep Learning World Models의 한계 극복: Dreamer와 같은 신경망 기반 world models는 강력하지만 엄청난 양의 training data를 요구하며, 학습 데이터 분포 밖의 새로운 상황(OOD)에 대한 일반화 능력이 떨어짐.
• Existing Symbolic Approaches의 확장성 문제 해결: WorldCoder와 같은 기존의 프로그램 기반 접근법은 전체 세계를 설명하는 단일(monolithic) 프로그램을 찾으려 시도함. 이는 탐색 공간이 너무 커서 단순한 Grid-world 수준을 넘어서는 복잡한 환경(Atari 등)으로 확장되지 못함.
• Modular & Data-Efficient Approach 제시: 복잡한 세계를 하나의 거대한 프로그램이 아닌, 수백 개의 작은 Programmatic Experts의 조합(Product)으로 모델링하여 데이터 효율성을 높이고, Atari와 같은 복잡한 환경에서도 작동하며 새로운 레벨로의 Zero-shot Generalization이 가능한 방법론을 제안함.

---

Key Contributions

• PoE-World Representation:
  • World Model을 Exponentially-weighted Product of Programmatic Experts로 표현함.
  • 수학적으로는 $P(next_state | history, action)$을 여러 expert 프로그램 확률의 곱으로 정의.
  • 각 expert는 "적에 닿으면 죽는다"와 같은 개별적인 인과 법칙(causal law)을 코드로 인코딩함.
• Hybrid Learning Algorithm:
  • **LLM (Large Language Models)**을 사용하여 관찰된 전이(transition) 데이터로부터 작은 Python 프로그램(experts)들을 합성(synthesis).
  • 이후 Gradient-based optimization (L-BFGS 등)을 사용하여 각 expert의 신뢰도(weight)를 최적화하고, 불필요한 expert는 가지치기(pruning)하는 2단계 학습 과정을 도입.
• Hierarchical Planner Integration:
  • 학습된 world model을 활용하기 위해, 객체 간 접촉(contact) 기반의 추상 그래프(abstract graph)를 생성하는 상위 레벨 planner와 구체적인 행동을 결정하는 하위 레벨 motion planner를 결합한 시스템 구축.
• Scalability & Complexity:
  • 기존 symbolic model이 처리하지 못했던 Montezuma's Revenge와 같은 복잡하고 확률적(stochastic)이며 부분 관찰(partially observable) 가능한 환경에서 작동하는 최초의 symbolic world model 구현.

---

Novelty

• Decomposition Strategy: "전체를 설명하는 하나의 프로그램"을 찾는 대신, "부분을 설명하는 여러 전문가 프로그램"을 찾아 조합하는 Divide and Conquer 전략을 World Modeling에 도입.
• Probabilistic Program Synthesis: LLM이 생성한 결정론적(deterministic) 코드들을 확률 분포로 해석하고, 이를 곱(Product) 형태로 결합하여 불확실성과 확률적 요소를 다루는 방식.
• Learning Efficiency: 1분 미만의 짧은 데모 영상만으로도 게임의 물리 법칙을 학습하고, 이를 통해 4000줄 이상의 코드로 구성된 정교한 world model을 구축함.

---

Experimental Highlights

• Datasets & Settings:
  • Games: Atari의 Pong, Montezuma's Revenge (MR).
  • Alt Versions: 학습된 물리 법칙의 일반화 성능을 검증하기 위해, 객체 수나 맵 구조를 변경한 Pong-Alt, MR-Alt 환경을 별도로 제작하여 테스트 (Zero-shot evaluation).
  • Input: 1000 프레임 미만의 짧은 데모 (성공적인 플레이가 아님).
• Baselines:
  • PPO: Model-free RL (100k steps & 20M steps).
  • ReAct: LLM을 직접 agent로 사용.
  • WorldCoder: 기존 SOTA symbolic world model.
• Key Results:
  • Montezuma's Revenge (MR): PoE-World + Planner는 100점(첫 번째 열쇠 획득)을 달성한 유일한 모델. 반면 PPO(20M steps 학습), ReAct, WorldCoder는 모두 0점 기록.
  • Generalization: MR-Alt(새로운 맵 구조)에서도 PoE-World는 추가 학습 없이 100점을 달성하며 강력한 Compositional Generalization 능력을 입증.
  • Sample Efficiency: 수백만 step을 학습한 PPO보다, 짧은 데모만 본 PoE-World의 성능이 우수하거나 대등함.
  • Policy Pre-training: PoE-World로 학습한 시뮬레이터 안에서 PPO를 사전 학습(Pre-training)시킨 후 실제 환경에 적용했을 때, 학습 속도가 획기적으로 빨라짐을 확인.

---

Limitations and Future Work

• Limitatons:
  • Dependency on Symbolic Input: 픽셀(Raw Pixel) 입력을 직접 처리하지 못하고, 객체 감지기(OCAtari)를 통해 추출된 symbolic state에 의존함. 즉, 비전 처리(Perception) 모듈이 완벽해야 함.
  • Exploration Problem: World Model 학습은 주어진 데모(demonstration)에 의존하며, 스스로 환경을 탐험하며 데이터를 수집하는 RL의 탐험(exploration) 문제는 다루지 않음.
  • Hard Constraints Necessity: 물리적으로 불가능한 상황(예: 벽 뚫기)을 방지하고 장기 계획(long-horizon planning)을 위해, 별도로 학습된 Hard Constraints가 필요했음 (특히 Montezuma's Revenge에서).
• Future Work:
  • Exploration via Program Testing: 프로그램 구조의 World Model을 활용하여, 코드의 분기(branch)를 테스트하듯이 환경을 효율적으로 탐험하는 새로운 탐색 기법 연구 가능성.
  • End-to-End Learning: 픽셀 입력으로부터 직접 프로그램을 생성하거나, 비전 모듈과 통합하는 연구.
  • Planner Efficiency: 현재의 Hierarchical Planner는 성능은 좋으나 계산 비용이 높으므로, 이를 최적화하는 연구.

---

Overall Summary

이 논문은 복잡한 환경을 하나의 거대한 프로그램이 아닌, 수백 개의 작은 Programmatic Experts들의 확률적 조합(Product of Experts)으로 모델링하는 PoE-World를 제안합니다. LLM을 이용한 코드 생성과 Gradient 기반 최적화를 결합하여, 매우 적은 데이터만으로도 Atari 게임(Montezuma's Revenge 등)의 물리 법칙을 정확히 학습하고, 이를 통해 맵이나 객체 구성이 바뀐 새로운 환경에서도 Zero-shot으로 적응하는 뛰어난 일반화 성능을 보여주었습니다. 이 연구는 기존 Deep RL의 데이터 비효율성과 Symbolic AI의 확장성 문제를 동시에 해결할 수 있는 Neuro-symbolic AI의 새로운 가능성을 제시하며, 향후 로봇 공학이나 복잡한 시뮬레이션 환경에서의 효율적인 계획 및 학습에 크게 기여할 수 있습니다.

---

Easy Explanation (쉬운 설명)

"한 명의 천재에게 모든 것을 맡기는 대신, 수백 명의 전문가 팀을 꾸리는 것과 같습니다."

• 기존 방식 (WorldCoder): "이 게임의 모든 규칙을 담은 두꺼운 백과사전 한 권을 써줘"라고 요청합니다. 규칙이 조금만 복잡해져도 책을 완성하기 어렵고, 내용이 틀리기 쉽습니다.
• 이 논문의 방식 (PoE-World):
  • "너는 사다리만 연구해", "너는 적만 연구해", "너는 중력만 연구해"라고 수백 명의 전문가(Programmatic Experts)에게 역할을 나눕니다.
  • 게임이 진행될 때, 각 전문가는 자신의 분야에 대해서만 "다음엔 이렇게 될 거야"라고 의견을 냅니다.
  • 이 의견들을 종합(Product)하여 가장 그럴듯한 미래를 예측합니다.
  • 만약 예측이 틀리면, 틀린 의견을 낸 전문가의 신뢰도(weight)를 낮춥니다.
• 결과: 이렇게 하니 복잡한 Montezuma's Revenge 같은 게임도 금방 배우고, 게임 맵이 바뀌어도(Generalization) "사다리 전문가는 여전히 사다리 규칙을 알기 때문에" 문제없이 적응할 수 있습니다.

 

 

 

 

Abstract

세상이 어떻게 작동하는지 배우는 것은 복잡한 environments에 적응할 수 있는 AI agents를 구축하는 데 핵심적입니다. deep learning에 기반한 전통적인 world models는 방대한 양의 training data를 요구하며, sparse observations로부터 지식을 유연하게 업데이트하지 못합니다.

Large Language Models (LLMs)를 사용한 program synthesis의 최근 발전은 source code로 표현된 world models를 학습하는 대안적인 접근 방식을 제공하여, 적은 데이터로도 강력한 generalization을 지원합니다. 현재까지 program-structured world models의 적용은 natural language 및 grid-world domains에 국한되어 있습니다.

우리는 LLMs에 의해 synthesized된 exponentially-weighted product of programmatic experts (PoE-World)로 world model을 표현함으로써, 복잡한 non-gridworld domains를 효과적으로 modeling하기 위한 새로운 program synthesis method를 소개합니다. 우리는 이 접근 방식이 단 몇 번의 observations만으로도 복잡하고 stochastic한 world models를 학습할 수 있음을 보여줍니다.

우리는 학습된 world models를 model-based planning agent에 embedding하여 평가하며, Atari의 Pong과 Montezuma's Revenge의 unseen levels에 대한 효율적인 performance와 generalization을 입증합니다. 우리는 code를 공개하고, 학습된 world models와 agent의 gameplay 영상을 https://topwasu.github.io/poe-world 에서 보여줍니다.

 

 

 

 

1 Introduction

지능형 agent는 자연 세계의 dynamics를 어떻게 표현해야 할까요? 우리는 효율적으로 학습할 수 있으면서도 stochasticity와 partial observability를 처리할 수 있을 만큼 충분히 유연하고, planning과 decision-making을 지원하는 representation을 원합니다. Dreamer와 같은 Neural network world models는 극도로 유연하지만, 인간에 비해 방대한 양의 training data를 요구합니다. 반면 WorldCoder와 같은 Symbolic world models는 세상이 작동하는 방식을 표현하기 위해 Python 프로그램을 생성합니다. 이러한 programmatic world models는 program synthesis가 neural network training보다 적은 데이터를 필요로 하기 때문에 data-efficient하지만, 세상이 작동하는 방식에 대한 모든 것을 설명하는 단일의 거대한 프로그램을 찾기 위해 discrete combinatorial search를 수행하기 때문에 단순한 gridworlds를 넘어 확장하는 데 어려움을 겪습니다.

 

우리는 마음을 상호 작용하는 전문가들의 커뮤니티로 보는 철학과 인지 과학의 오랜 관점에서 영감을 얻었습니다. 이러한 modular 구성은 뇌 시스템의 기능적 전문화부터 특정 기술의 뚜렷한 학습 궤적에 이르기까지 자연 지능의 여러 척도에 걸쳐 분명하게 나타납니다. 우리는 이러한 modular 관점을 학습된 개념을 symbolic programs로 modeling하는 Program Synthesis라는 학습의 계산적 paradigm과 통합합니다. 우리는 world models를 학습하는 것에 대한 새로운 계산적 설명을 제안함으로써 이 연구의 맥락을 확장합니다. 이는 연습을 통해 정제되고 유연한 목표 지향적 행동을 지원하기 위해 compositionally 재사용되는 context-specific expert programs의 획득으로서 학습을 설명합니다.

 

알고리즘적으로 우리의 핵심 idea는 world program을 학습하는 문제를 수백 개의 작은 프로그램을 학습하는 것으로 분해하는 것입니다. 학습된 각각의 프로그램들은 서로 다른 causal 법칙을 인코딩하며, 우리는 이를 확률적으로 통합하여 미래의 observations를 예측합니다 (Figure 1a). 이는 우리의 world knowledge를 더 modular하고 더 쉽게 학습할 수 있게 만드는데, 그 이유는 우리가 더 이상 모든 것을 한 번에 처리하는 단일의 거대한 프로그램을 탐색하지 않기 때문입니다. 우리가 PoE-World (Product of programmatic Experts)라고 부르는 그 결과 system은 Montezuma's Revenge와 같은 복잡한 Atari 게임에서 짧은 demonstration만으로도 planning과 reinforcement learning (RL)을 정확하게 지원하는 정교한 world models를 구축할 수 있습니다. PoE-World는 프로그램들의 product가 확률적이기 때문에 stochasticity를 처리하며, 우리가 보여주듯이 나아가 partial observability까지 처리합니다. 우리가 아는 한, 이것은 이러한 복잡성을 가진 environments에 대해 symbolic world model이 학습된 첫 번째 사례입니다.

 

중요한 점은, PoE-World가 세밀한 pixel-level 움직임을 model하지만, pixel-level의 visual appearance를 model하지는 않으며 대신 object detector로부터 얻은 symbolic observations를 가정한다는 것입니다. model-based reinforcement learning과 달리, PoE-World는 효율적인 탐색(exploration)을 시도하지 않고, demonstrated trajectory로부터 충실하게 학습하는 데 집중합니다 (Figure 1b). 마지막으로, world models가 궁극적으로는 planning에 사용되지만 (Figure 1c), PoE-World는 근본적으로 world modeling에 초점을 맞추며, planning 자체의 어려운 계산 문제를 해결하는 것에는 초점을 맞추지 않습니다.

이러한 한계들에도 불구하고, 우리는 PoE-World가 새로운 environment에 대한 제한된 demonstrations가 주어졌을 때 새로운 상황으로 compositionally generalize할 수 있는 작동 가능한 world model을 빠르게 조립하는 핵심적인 학습 문제를 다루고 있다고 봅니다 (Figure 1d). 우리는 다음과 같은 기여(contributions)들을 강조합니다:

1. symbolic world models를 위한 PoE-World representation과 learning algorithm.
2. 두 가지 대표적인 Atari 게임인 Pong과 Montezuma's Revenge에 대한 PoE-World의 경험적 연구를 통해, deep RL과 비교하여 우수한 학습 효율성을 보여주고 state-of-the-art symbolic model-based RL에 비해 향상된 scalability를 입증합니다. PoE-World는 새로운 게임 레벨과 게임 변형들에 대해 zero-shot으로 generalize하는 4000줄 이상의 프로그램을 synthesize할 수 있습니다.
3. PoE-World의 world models를 planning-based decision making에 사용하는 방법과 deep RL을 위한 시뮬레이션된 pretraining environment로 사용하는 방법에 대한 시연.

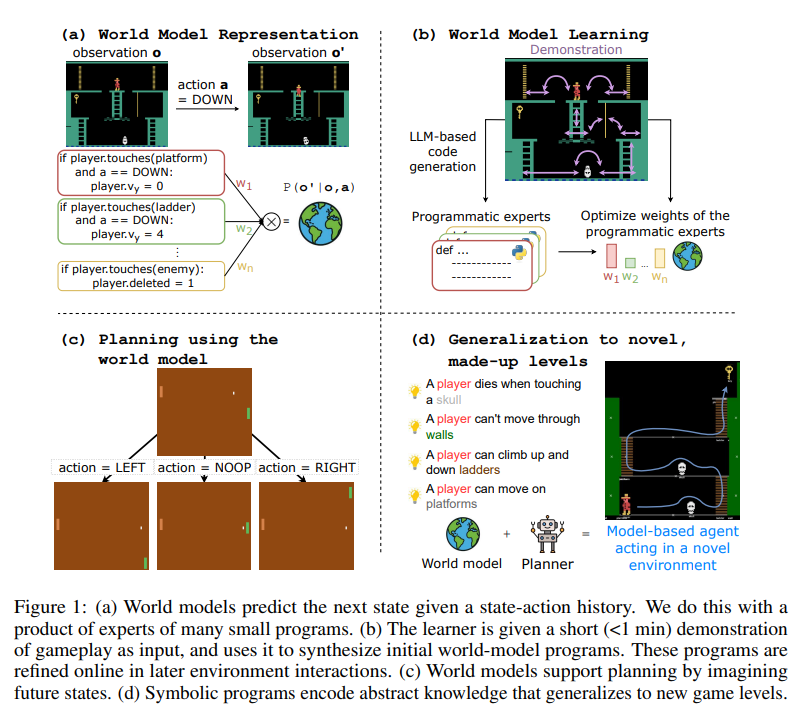
(a) World Model Representation 주어진 state-action history를 바탕으로 다음 state를 예측하는 과정을 보여줌. 전체 규칙을 하나의 덩어리로 처리하는 대신, 여러 개의 작은 programmatic experts(코드 조각들)의 조합을 사용함. 이미지 좌측을 보면 플레이어가 사다리에 닿았을 때, 플랫폼에 닿았을 때, 적에게 닿았을 때 작동하는 개별 파이썬 조건문들이 각각 가중치(W1, W2, Wn)를 가지고 있음. 이들이 확률적으로 곱해져서(product) 최종적인 예측 모델을 형성하는 구조임.

(b) World Model Learning AI가 1분 미만의 짧은 게임 플레이 demonstration 영상을 입력으로 받는 모습을 보여줌. 이를 바탕으로 LLM-based code generation을 실행하여 초기 programmatic experts를 합성해 냄. 그 후 실제 환경에서 최적화 과정을 거쳐 각 프로그램 전문가들의 가중치(weights)를 조정하여 학습을 완성함.

(c) Planning using the world model 학습이 완료된 world models가 미래의 states를 시뮬레이션하여 planning을 수행하는 과정을 보여줌. 퐁(Pong) 게임을 예시로, 현재 화면에서 LEFT, NOOP, RIGHT action을 취했을 때 각각 어떤 미래 화면이 펼쳐질지 트리 구조로 예측하고 있음.

(d) Generalization to novel, made-up levels 학습된 Symbolic programs가 어떻게 새로운 환경에 일반화(generalize)되는지 보여줌. 해골에 닿으면 죽는다, 벽을 통과할 수 없다 등 앞서 학습한 추상적인 지식들(World model)과 Planner가 결합함. 그 결과, 한 번도 플레이해 본 적 없는 완전히 새로운 구조의 맵에서도 Model-based agent가 스스로 경로를 계획하고 움직일 수 있음을 나타냄.

 

 

 

 

 

논문 핵심 정리 노트: 1. Introduction

연구 배경 및 기존 방법론의 한계

• Neural network world models (예: Dreamer): 유연하지만 인간과 비교할 때 방대한 양의 training data가 필수적임.
• Symbolic world models (예: WorldCoder): Program synthesis를 활용해 data-efficient 하지만, 세상의 모든 규칙을 담은 '단일 거대 프로그램'을 찾기 위해 discrete combinatorial search를 수행하므로 단순한 gridworlds 이상으로 scale-up 하기 어려움.

핵심 제안: PoE-World (Product of programmatic Experts)

• Modular Program Synthesis: 인지과학의 모듈성(전문가들의 커뮤니티) 개념을 차용. World models를 하나의 거대한 프로그램이 아닌, 수백 개의 context-specific expert programs로 분해하여 학습.
• 확률적 통합 (Probabilistic Aggregation): 학습된 각각의 작은 프로그램들은 서로 다른 causal 법칙을 인코딩하며, 이들을 확률적으로 곱하여(product) 미래의 observations를 예측함. 이를 통해 stochasticity와 partial observability를 효과적으로 처리.

PoE-World의 특징 및 한계 (연구의 Scope)

• 짧은 demonstration만으로도 Pong, Montezuma's Revenge 같은 복잡한 Atari 게임에서 planning과 RL을 지원하는 정교한 모델 구축 가능 (이 정도 복잡도 환경에서 symbolic world model이 적용된 첫 사례).
• 가정: pixel-level visual appearance를 직접 모델링하지 않고, object detector에서 추출된 symbolic observations를 기반으로 pixel-level movement를 모델링함.
• 초점: Efficient exploration이나 복잡한 planning 알고리즘 자체를 푸는 것이 아니라, 주어진 demonstrated trajectory로부터 faithful하게 world modeling을 수행하고 새로운 상황에 compositionally generalize 하는 것에 집중.

주요 Contributions

1. Symbolic world models를 위한 새로운 PoE-World representation 및 learning algorithm 제안.
2. Deep RL 대비 압도적인 학습 효율성, 기존 SOTA symbolic model-based RL 대비 뛰어난 scalability 입증 (4000줄 이상의 프로그램 합성 및 unseen levels/variations에 대한 zero-shot generalization 달성).
3. 학습된 world models를 planning-based decision making 및 deep RL을 위한 시뮬레이션 pretraining environment로 활용하는 구체적인 시연 제공.

---

쉬운 설명 : 1 Introduction

AI가 게임 같은 새로운 환경에 던져졌을 때, 세상이 어떻게 돌아가는지(물리법칙이나 게임 규칙 등) 스스로 파악하게 만드는 연구입니다.

기존에는 두 가지 극단적인 방법이 있었습니다. 첫째는 엄청나게 많은 플레이 데이터를 AI에게 먹여서 패턴을 통째로 외우게 하는 방식(Neural network 방식)이었고, 둘째는 AI가 직접 세상의 규칙을 묘사하는 '하나의 거대한 파이썬 코드'를 짜게 하는 방식(Symbolic 방식)이었습니다. 전자는 데이터가 너무 많이 필요했고, 후자는 팩맨처럼 조금만 게임이 복잡해져도 경우의 수가 너무 많아져서 AI가 코드를 완성하지 못하고 뻗어버리는 문제가 있었습니다.

이 논문은 **"모든 규칙을 완벽하게 담은 하나의 거대한 코드를 짜려고 하지 말고, 특정 상황에만 전문적으로 반응하는 '작은 코드 조각(전문가)' 수백 개를 만들어서 합치자!"**라는 아주 영리한 아이디어를 냈습니다.

예를 들어 '캐릭터가 벽에 부딪혔을 때'를 담당하는 코드, '적과 만났을 때'를 담당하는 코드를 따로따로 만든 뒤, 상황이 발생했을 때 이 작은 코드들의 의견을 확률적으로 종합해서 다음 장면을 예측하는 것입니다. 이렇게 문제를 잘게 쪼개서 접근했더니, 기존에는 불가능했던 '몬테주마의 복수' 같이 아주 복잡한 고전 게임에서도 AI가 단 몇 번의 플레이 영상만 보고 게임의 모든 규칙을 완벽하게 코드로 짜냈습니다. 심지어 한 번도 본 적 없는 새로운 맵에 던져져도 이 규칙들을 조립해서 능숙하게 게임을 풀어나가는 놀라운 결과를 보여줍니다.

 

 

 

 

2 Background: World Model Learning

sequential decision-making 문제는 $(O, A, P, R)$ 로 설명될 수 있으며, 여기서 $O$는 observation space, $A$는 action space, $P$는 environment dynamics $P = p_{env}(o_{t+1}|o_{1:t}, a_{1:t})$ ($o \in O$ 및 $a \in A$), 그리고 $R$은 reward function입니다. 이러한 full-history environment formulation은 수학적으로 Partially Observable Markov Decision Process (POMDP) formulation과 동일합니다. $P$가 agent에게 알려지지 않은 설정에서, agent는 environment와 상호작용하고 timestep $t$에서 transitions $(o_t, a_t, o_{t+1}, r_t)$를 관찰함으로써 학습합니다.

우리는 관찰된 trajectories $D = \{\tau_i\}_{i=1}^n$ 가 주어졌을 때 실제 알려지지 않은 environment dynamics $P = p_{env}(o_{t+1}|o_{1:t}, a_{1:t})$를 근사하는 world model $\hat{P} = p_{model}(o_{t+1}|o_{1:t}, a_{1:t})$를 학습하는 데 초점을 맞춥니다. 여기서 각 trajectory는 특정 $T$에 대한 observations와 actions의 sequence $\tau = (o_{1:T+1}, a_{1:T})$입니다 ($r_{1:T}$ 또한 trajectory의 일부이지만 단순성을 위해 생략합니다). 학습된 world model은 이후 model-based agent에 의해 lookahead planning이나 RL training을 통해 environment에서 행동(act)하는 데 사용될 것입니다.

우리는 world modeling 문제를 optimization 문제, 특히 empirical risk minimization으로 취급합니다:

$$p^*_{model} = \arg\min_{p_{model}} \sum_{(o_{1:T+1},a_{1:T}) \in D} \sum_{t=1}^T \ell(p_{model}; o_{1:t+1}, a_{1:t})$$

여기서 $\ell$은 negative log likelihood function $\ell(p_{model}; o_{1:t+1}, a_{1:t}) = - \log p_{model}(o_{t+1}|o_{1:t}, a_{1:t})$ 와 같은 loss function입니다.

model-based reinforcement learning 문헌의 이전 연구들은 $p_{model}$을 parametric model $p_{model} = p_{\theta}$로 정의하기 위해 convolutional 및 recurrent neural networks, transformers, 그리고 diffusion models를 포함한 다양한 deep neural network architectures를 사용했습니다. 그런 다음, $\theta$는 gradient descent를 통해 최적화(optimized)됩니다. 이러한 접근 방식의 약점은 sample efficiency와 generalization이 부족하다는 것입니다. 예를 들어, Diamond는 거의 100시간 분량의 observations에 대해 학습한 후에도 플레이어가 벽을 통과하거나 텔레포트할 수 있다고 상상하는 것과 같은 failure modes를 가지고 있습니다.

다른 연구들은 code world model을 synthesize하기 위해 Large Language Models (LLMs)를 활용하는데, 이는 programmatic $p_{model}$을 탐색하는 것으로 볼 수 있습니다. 이러한 LLM-based code generation 알고리즘들은 deep learning 접근 방식보다 더 sample efficient하며 더 체계적으로 extrapolate합니다. 그러나, 이들은 아직 단순한 text-based 및 gridworld 게임들을 넘어서 성공을 거두지 못했습니다.

논문 핵심 정리 노트: 2. Background: World Model Learning

1. World Modeling의 수학적 정의 (ERM 관점)

• 목표: Agent가 관찰한 trajectories $D$를 바탕으로 실제 환경의 dynamics $P$를 근사하는 world model $\hat{P} = p_{model}(o_{t+1}|o_{1:t}, a_{1:t})$를 학습하는 것.
• 접근: 이 과정을 Empirical Risk Minimization (ERM) 문제로 치환하여, negative log-likelihood 등의 loss function을 최소화하는 방향으로 최적화함.

2. 기존 방법론 1: Deep RL (Neural Network 기반)

• 방식: Convolution, RNN, Transformer, Diffusion 등을 활용해 모델을 매개변수화($p_\theta$)하고 Gradient Descent로 최적화.
• 치명적 한계: Sample efficiency와 generalization 능력이 매우 떨어짐.
  • 사례: SOTA 모델인 Diamond조차 100시간 이상의 관찰 데이터를 학습하고도 플레이어가 벽을 통과하거나 순간이동하는 등 기본적인 물리법칙(Dynamics)을 제대로 상상하지 못하는 failure mode를 보임.

3. 기존 방법론 2: LLM-based Code Generation (Symbolic 기반)

• 방식: LLM을 활용해 environment dynamics를 묘사하는 programmatic $p_{model}$ (소스 코드)을 직접 탐색하고 합성함.
• 장점: Deep learning 방식 대비 압도적인 sample efficiency를 보이며, 훨씬 체계적으로 extrapolate(외삽) 가능함.
• 치명적 한계: 탐색 공간의 복잡도 문제로 인해 text-based 게임이나 단순한 gridworld 수준을 벗어난 복잡한 환경에서는 성공한 사례가 없음.

💡 연구자를 위한 핵심 요약

이 섹션은 단순히 POMDP를 설명하는 데 그치지 않고, 왜 새로운 접근이 필요한지 강력한 빌드업을 제공합니다. 기존 Deep RL은 **'복잡한 환경은 소화하지만 물리법칙 일반화에 실패'**하고, 기존 Symbolic RL은 **'일반화는 잘하지만 복잡한 환경을 소화하지 못함'**을 지적하며, 본 논문의 PoE-World가 이 두 가지 한계를 모두 극복할 스위트스팟을 노리고 있음을 명확히 합니다.

---

쉬운 설명 : 2 Background: World Model Learning

이 섹션은 **"왜 지금까지 AI가 게임 속 세상을 완벽하게 이해하는 데 실패했는가?"**에 대한 배경 설명입니다. AI가 다음 장면을 예측하도록 가르치는 기존의 두 가지 방식과 그 뚜렷한 한계점을 꼬집고 있습니다.

1. 딥러닝(신경망) 방식의 한계: "감으로 때려 맞추다 보니 엉뚱한 상상을 함"
2. 최신 AI 기술(트랜스포머, 디퓨전 등)을 써서 100시간 넘게 게임 영상을 보여주며 학습시켜도, AI는 물리법칙을 '이해'하는 게 아니라 데이터의 '패턴'만 외웁니다. 그래서 처음 보는 상황에 놓이면 캐릭터가 벽을 뚫고 지나가거나 텔레포트해 버리는 등 상식적으로 말도 안 되는 예측을 해버립니다. (데이터가 아무리 많아도 일반화가 안 됨)
3. 코드 생성(심볼릭) 방식의 한계: "규칙은 잘 짜는데, 조금만 복잡해져도 포기함"
4. AI에게 아예 게임의 작동 규칙을 파이썬 코드 같은 '공식'으로 짜보라고 시키는 방식입니다. 이 방식은 공식을 한 번 제대로 짜면 절대 벽을 뚫는 식의 바보 같은 실수를 하지 않습니다. 하지만 팩맨이나 바둑판 같은 아주 단순한 환경에서만 통할 뿐, 몬테주마의 복수처럼 화면이 조금만 복잡해져도 AI가 전체 규칙을 아우르는 코드를 짜내지 못하고 과부하가 걸려버립니다.

결론적으로, 데이터 낭비 없이 완벽한 규칙을 찾아내면서도(코드 생성 방식의 장점), 복잡한 화면과 액션이 있는 게임에서도 작동하는(딥러닝 방식의 장점) 완전히 새로운 돌파구가 필요하다는 것을 설명하는 단계입니다.

 

 

 

 

3 Modeling the World as a Product of Programmatic Experts (PoE-World)

기존 world model learning 방식의 한계를 해결하기 위해, 우리는 world models를 exponentially-weighted Products of programmatic Experts (PoE-World)로 표현할 것을 제안하며, 이는 LLM code generation을 활용하는 probabilistic world models의 sample-efficient하고 scalable한 학습을 가능하게 합니다. Figure 1은 이 섹션에서 논의되는 representation과 learning algorithm을 모두 시각화합니다.

3.1 World Model Representation: Product of Programmatic Experts (PoE-World)

exponentially weighted Products of programmatic Experts (PoE-World)로 표현되는 World models는 수학적으로 다음과 같이 설명될 수 있습니다:

$$p_\theta(o_{t+1}|o_{1:t}, a_{1:t}) \propto \prod_i p^{expert}_i(o_{t+1}|o_{1:t}, a_{1:t})^{\theta_i} \quad (2)$$

여기서 $p^{expert}_i$는 programs이고 $\theta_i$는 그와 연관된 scalar weights입니다.

이러한 representation은 modularity와 compositionality를 가능하게 합니다. 이는 복잡한 environmental dynamics를 포착하기 위해 많은 작은 programs를 하나의 완전한 world model로 구성(compose)할 수 있게 해줍니다 (Figure 2 참조). 우리는 각 program을 세상의 특정 측면에 대한 의견을 표현하는 expert로 생각할 수 있습니다. 예를 들어, video game environment를 modeling하는 맥락에서, 한 expert는 "만약 플레이어가 해골에 닿으면, 플레이어는 죽는다"를 인코딩할 수 있고, 다른 expert는 "플레이어가 플랫폼에 있을 때 action이 LEFT라면, 플레이어의 x축 속도는 -2이다"를 인코딩할 수 있습니다. 전자의 expert는 플레이어의 움직임에 대한 의견을 내지 않으며, 후자는 플레이어의 죽음 조건에 대해 언급하지 않습니다.

factored state representation은 다루기 쉬운(tractable) inference를 산출합니다. 우리는 각 객체가 bounding box와 속도(velocities)를 가지며 각각이 별도의 slot, attribute 또는 feature로 저장되는 object-centric state를 가정합니다. 우리는 지금까지의 history가 주어졌을 때 이러한 각 feature를 conditionally independent한 것으로 취급합니다. 이러한 independence 가정은 Equation (2)를 다루기 쉽게 만드는데, 각 feature에 대해 별도의 normalizing constant를 계산할 수 있기 때문입니다. 구체적으로, $f$를 다음 observation $o_{t+1}$의 다양한 object features에 대한 인덱스라고 하고, $o^f$를 feature $f$가 있는 $o$의 인덱싱이라고 합시다. 그러면,

$$p_\theta(o_{t+1}|o_{1:t}, a_{1:t}) = \prod_f \frac{1}{Z_f} \prod_i p^{expert}_i(o^f_{t+1}|o_{1:t}, a_{1:t})^{\theta_i} \quad Z_f = \sum_{o^f} \prod_i p^{expert}_i(o^f|o_{1:t}, a_{1:t})^{\theta_i}$$

POMDP formulation 대비 full-history formulation의 이점. full-history environment formulation은 history를 Markov latent state로 압축하는 POMDP와 공식적으로 동일합니다. 우리는 world models를 더 modular하게 만들기 때문에 history formulation을 사용합니다. global latent variables를 학습하는 것은 모든 expert가 latent state에 condition되기 때문에 모든 experts를 뒤엉키게(entangle) 만들 것입니다. 따라서 새로운 latent variable(예: "플레이어가 얼마나 오랫동안 떨어지고 있었는지")을 학습하는 것은 모든 expert의 input/output space를 변화시켜 모든 program의 구조에 대한 global joint updates를 필요로 합니다 (예: "플레이어가 죽었는지"에 대한 expert가 업데이트되어야 함). history formulation은 독립적인 메커니즘들의 독립적인 학습을 허용합니다.

Hard constraints. Atari (그리고 현실 세계)는 사실상 학습 가능한(effectively learnable) 어떤 program으로든 완벽하게 시뮬레이션하기에는 너무 복잡합니다. 따라서 우리의 probabilistic model은 가능한 미래의 집합을 over-approximate하는 경향이 있으며, 모호하고(fuzzy) 근사적인(approximate) 예측을 제공합니다. 예를 들어, Montezuma's Revenge에서 아래로 떨어져 땅에 착지하는 물리를 완벽하게 modeling하는 대신, 우리는 일반적인 하강 궤적을 예측합니다. 이상적으로 그 궤적은 플레이어가 땅에 평평하게 착지하고 절대 땅 속으로 가라앉지 않는다는 constraint를 완벽하게 강제(enforce)해야 하지만, 아래로 떨어지는 것에 대한 fuzzy stochastic expert는 그 constraint를 위반할 수 있습니다. 따라서 model의 출력(outputs)을 더 날카롭게(sharpen) 하기 위해, 우리는 하드 제약 조건들(hard constraints)의 모음 ${c_j}$를 추가로 학습하며, 여기서 $c_j : O \rightarrow \{0, 1\}$ 입니다:

$$p_\theta(o_{t+1}|o_{1:t}, a_{1:t}) \propto \prod_i p^{expert}_i(o_{t+1}|o_{1:t}, a_{1:t})^{\theta_i} \cdot \mathbf{1}\left[\bigvee_j c_j(o_{t+1})\right] \quad (3)$$

우리는 Section A.1에서 hard constraints에 대해 더 논의하고 구체적인 예시들을 제공합니다.

Multi-timestep predictions. 우리는 eq. (2)에서 programmatic experts와 세상을 next-timestep observations에 대한 distributions로 표현합니다. 다른 timestep에서의 multi-step expert의 예측이 독립적이라고 가정함으로써, multi-timestep expert $p^{expert}(o_{t+1:t+H}|o_{1:t}, a_{1:t})$를 next-timestep experts의 product로 재구성하는 것 또한 마찬가지로 가능합니다:

$$p^{expert}(o_{t+1:t+H}|o_{1:t}, a_{1:t}) = \prod_{k=1}^H p^{expert}(o_{t+k}|o_{1:t}, a_{1:t}) \quad (4)$$

3.2 World Model Learning: Program Synthesis and Weight Optimization

우리는 demonstration trajectory로 시작하여 world model을 학습한 다음, 그 model에 따라 세상에서 행동(act)하기 시작합니다. agent가 행동함에 따라 더 많은 trajectory 데이터를 수집하고, 이를 사용하여 자신의 model을 업데이트하거나 "디버깅(debug)"합니다. 구체적으로, 학습은 다음과 같이 진행됩니다:

Step 1: 관찰된 trajectories $D = \{\tau_i\}_{i=1}^n$가 주어졌을 때 programmatic experts $\{p^{expert}_i\}_{i=1}^m$를 Synthesize함.

Step 2: gradient-based optimizer를 사용하여 eq. (5)에 따라 experts의 weights $\theta$를 Fit함.

Step 3: weights가 임계값(threshold) $\delta$ 미만인 experts를 Remove함.

Step 4: 관찰된 trajectories가 업데이트될 때마다 Step 1-3을 Repeat함.

Generating program experts. 이전 연구들에 이어, 우리는 Large Language Models (LLMs)를 우리의 Python program generator로 채택합니다. 우리는 LLM prompt에 transitions의 작은 배치(batch) $(o_{t:t+H+1}, a_{t:t+H})$를 입력하여 programmatic experts ${p^{expert}_i}$를 생성(produce)합니다.

Figure 2는 우리가 작은 Python programs를 observations에 대한 distributions로 어떻게 해석하는지 보여줍니다. 우리가 distributions를 지정하기 위해 probabilistic programs를 synthesize하도록 LLMs에게 요청할 수도 있지만, 우리는 LLMs가 단순하고 deterministic한 Python programs를 synthesize하도록 하는 것이 훨씬 더 효과적이라는 것을 발견했습니다. 이는 아마도 일반적인 Python 코드가 LLM training data에 훨씬 더 prevalent하기 때문일 것입니다. 우리는 observation이 객체(objects)들의 리스트로 표현되며, 각 객체가 x/y 속도(velocity) 및 가시성(visibility)이라는 속성(attributes)을 갖는다고 가정합니다. 그러면, observations에 대한 distribution은 각 객체의 attributes에 대한 distribution입니다. Python program을 distribution으로 해석하기 위해, Section 3.1에서 언급했듯이 모든 객체 attributes가 full history가 주어졌을 때 conditionally independent하다고 가정하고, program에 의해 설정된 모든 객체 attributes를 주어진 값에 single peaks를 갖는 distributions로 변환합니다. 그런 다음 대체 값(alternative values)들에 대해 non-zero probabilities를 보장하기 위해 distributions에 노이즈를 추가합니다. program에 의해 값이 설정되지 않은 모든 객체 attributes는 가능한 모든 값에 대해 uniform distributions를 따릅니다: 결과적으로, 단일 if-condition이 있는 experts (fig. 2)는 if-condition이 만족되지 않을 때 uniform distribution을 산출합니다.

Gradient-based Weights Optimization. $\{p^{expert}_i\}_{i=1}^m$를 얻고 나면, maximum likelihood estimation을 수행하여 $\theta$를 얻을 수 있습니다:

$$\theta^* = \arg\max_\theta \sum_{(o_{1:T+1},a_{1:T}) \in D} \sum_{t=1}^T \log p_\theta(o_{t+1}|o_{1:t}, a_{1:t}) \quad (5)$$

이 방정식은 $p_{model}$이 parametric form $p_{model} = p_\theta$를 갖게 하고 loss function으로 negative log likelihood를 선택함으로써 eq. (1)을 구체화(instantiate)합니다. 우리는 weights를 최적화하기 위해 어떤 gradient-based optimizer든 사용할 수 있습니다. 우리는 데이터가 적고 parameters가 적기 때문에 Adam이나 SGD보다 더 잘 작동했던 L-BFGS를 사용합니다.

마지막으로, weights가 임계값(threshold) $\delta$ 미만인 experts는 world model에서 제거됩니다. 우리는 새로운 observations가 있을 때마다 이 루프를 반복합니다. Section A.1은 전체 알고리즘 세부 사항을 포함합니다.

3.3 World Model Usage: RL in Simulation and Planning with World Model

world modeling의 중요한 목표는 decision-making을 돕는 것입니다. 우리는 world models를 사용하는 이러한 두 가지 방법을 고려합니다. 첫째, world model은 reinforcement learning을 위한 simulator 역할을 할 수 있습니다. 이는 RL policy learning을 더 sample efficient하게 만드는데, 왜냐하면 실제 environment와의 상호작용으로부터 world model을 빠르게 학습할 수 있고, 이 model이 실제 environment를 대체하기 때문입니다. 이후의 policy learning은 world model 안에서 이루어질 수 있으며, 실제 environment와의 추가적인 상호작용의 필요성을 제거(obviating)합니다. 실제로는(In practice), world model에서의 pretraining 이후에도 reinforcement learning을 계속합니다. 공식적으로, 우리는 observation history를 입력받아 action을 출력하는 policy $\pi : O^* \rightarrow A$를 학습합니다.

대안적으로, world models는 lookahead planning에 사용될 수 있습니다. reward function $R$이 주어졌을 때, 이전의 observations $o_{1:t}$와 actions $a_{1:t-1}$가 주어지면 optimal action sequence를 탐색함으로써 $H$ timesteps의 horizon에 대해 planning을 합니다:

$$a^*_{t:t+H} = \arg\max_{a_{t:t+H}} \mathbb{E}_{p_\theta(o_{t+1:t+H}|o_{1:t},a_{1:t+H})} \left[ \sum_{k=0}^{H-1} R(o_{t+k+1}; o_{1:t+k}, a_{1:t+k}) \right]$$

여기서 $p_\theta(o_{t+1:t+H}|o_{1:t}, a_{1:t+H}) = \prod_{k=0}^{H-1} p_\theta(o_{t+k+1}|o_{1:t+k}, a_{1:t+k})$ 입니다.

우리의 world models가 long-horizon decision-making을 안내하는 것을 돕기 위해, 우리는 task and motion planning (TAMP)에서 영감을 받은 hierarchical planner를 구현합니다. 이는 먼저 객체 접촉(object contact)으로 정의된 high-level abstract state space에서 plan을 세운 다음, 학습된 world model을 사용하여 그 plans를 실제 Atari 버튼 누르기(button presses)로 낮춥니다(lowers) (Figure 3, Section A.2). 그 결과물인 agent를 우리는 PoE-World + Planner로 표기합니다.

 

 

 

 

 

 

 

Figure 2 설명: 프로그램 기반 전문가들의 확률 분포 해석 및 결합

• 단순한 Python 프로그램들이 어떻게 확률 분포(distributions)로 해석되고 결합되어 다음 timestep의 객체 위치를 예측하는지 보여주는 heat map 예시입니다.
• 플레이어가 RIGHT action을 취하는 상황에서 세 개의 programmatic experts가 각기 다른 예측과 가중치(weights)를 제시합니다.
  • $p^{expert}_1$ ($w=0.2$): 플랫폼에 닿아 있고 오른쪽으로 이동하므로 $v_x = 2$를 제안합니다.
  • $p^{expert}_2$ ($w=0.5$): 같은 조건에서 조금 더 빠른 $v_x = 3$을 제안합니다.
  • $p^{expert}_3$ ($w=0.4$): 사다리에 닿아 있으므로 위아래 이동이 없는 $v_y = 0$을 제안합니다.
• 가로축과 세로축의 붉은색 띠가 겹치는 영역이 모든 전문가들의 예측이 결합된(product) 지점이며, 이 교차점이 다음 timestep에서 플레이어가 위치할 확률이 가장 높은 곳(Most likely player's position)이 됩니다.

 

 

 

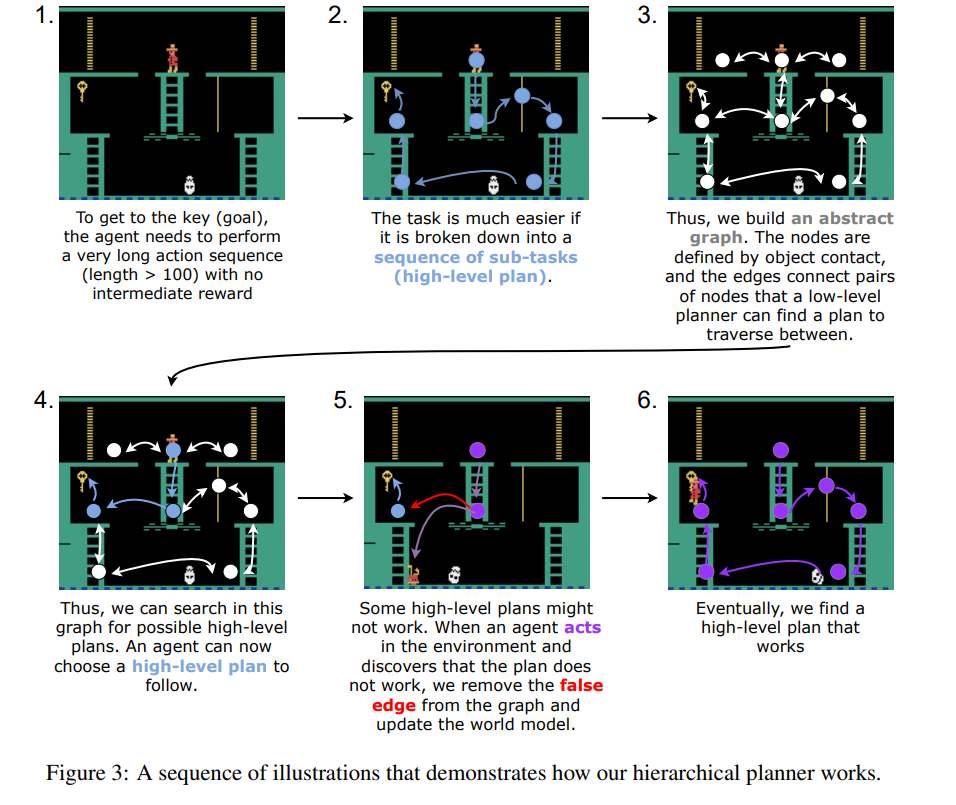
Figure 3 설명: Hierarchical planner의 단계별 작동 방식

• 1단계: agent가 중간 보상 없이 최종 목표(열쇠)에 도달하기 위해 100회 이상의 매우 긴 action sequence를 수행해야 하는 어려운 상황을 보여줍니다.
• 2단계: 이 복잡한 전체 작업을 여러 개의 중간 목표(sub-tasks)를 거치는 high-level plan으로 잘게 쪼개어 문제를 단순화합니다.
• 3단계: 객체 간의 접촉 지점(사다리 끝, 플랫폼 끝 등)을 노드(nodes)로 삼고, low-level planner가 이동할 수 있는 구간을 엣지(edges)로 연결하여 추상적인 그래프(abstract graph)를 구축합니다.
• 4단계: 구축된 그래프 내에서 목표 지점까지 도달할 수 있는 실현 가능한 high-level plans를 탐색하고 선택합니다.
• 5단계: agent가 실제 환경에서 행동(acts)을 수행하다가 특정 구간의 계획이 불가능함을 깨달으면(false edge), 해당 엣지를 그래프에서 제거하고 world model을 업데이트합니다.
• 6단계: 오류를 수정하고 다시 탐색하는 과정을 거쳐 마침내 끝까지 성공적으로 작동하는 최적의 high-level plan을 찾아냅니다.

 

 

논문 핵심 정리 노트: 3. Modeling the World as a Product of Programmatic Experts (PoE-World)

1. 핵심 아이디어: PoE-World Representation

• 개념: 복잡한 거대 모델 하나를 학습하는 대신, 수많은 작은 programmatic experts (파이썬 코드 조각)들의 지수 가중 곱(exponentially-weighted product)으로 world models를 정의.
• 수식:
  • 각 $p^{expert}_i$는 특정 상황(예: "해골에 닿았을 때", "사다리에서 위로 갈 때")만을 묘사하는 프로그램.
  • $\theta_i$는 해당 전문가의 신뢰도(weight).
•  
• $$p_\theta(o_{t+1}|o_{1:t}, a_{1:t}) \propto \prod_i p^{expert}_i(o_{t+1}|o_{1:t}, a_{1:t})^{\theta_i}$$
• Factored State & Tractable Inference: Object-centric state를 가정하여 각 feature(위치, 속도 등)를 conditionally independent하게 취급. 덕분에 전체 분포를 계산할 때 각 feature별로 따로 정규화(normalizing)가 가능해져 계산 복잡도(tractability)가 해결됨.
• POMDP 대신 Full-history를 쓰는 이유: POMDP처럼 하나의 global latent state로 압축해버리면, 새로운 변수가 추가될 때마다 모든 expert의 input/output 구조를 갈아엎어야 함. Full-history를 쓰면 각 expert가 완전히 독립적으로 학습되고 작동할 수 있어 modularity가 극대화됨.
• Hard Constraints의 도입: 확률적 예측은 필연적으로 fuzzy함을 동반함(예: 땅에 착지하는 궤적을 뭉뚱그려 예측). "캐릭터가 땅을 뚫고 들어갈 수 없다"와 같은 절대적인 물리법칙을 보정하기 위해 boolean hard constraints $c_j$를 지시 함수(indicator function)로 곱하여 예측 분포를 날카롭게(sharpen) 만듦.

2. World Model Learning (학습 프로세스)

• 1단계 (Synthesis): 짧은 trajectories 배치를 LLM prompt로 넣어 초기 파이썬 프로그램들(experts)을 생성.
  • Tip: LLM에게 복잡한 확률 분포 코드를 짜라고 하는 것보다, 단순하고 deterministic한 파이썬 코드를 짜게 한 뒤, 모델 내부에서 약간의 노이즈를 섞어 확률 분포로 변환하는 것이 훨씬 성능이 좋음. (코드가 커버하지 않는 속성은 uniform distributions 처리)
• 2단계 (Optimization): 수집된 데이터를 바탕으로 negative log likelihood를 최소화하도록 weights($\theta$)를 최적화. 파라미터가 적기 때문에 Adam 대신 L-BFGS optimizer 사용.
• 3단계 (Pruning): 신뢰도 가중치가 임계값($\delta$) 이하로 떨어진 쓸모없는 expert는 과감히 삭제(Remove).
• 이 과정을 새로운 데이터가 들어올 때마다 반복.

3. World Model Usage (활용 방안)

• RL Simulator로 활용: 실제 환경에서 데이터를 더 모을 필요 없이, 완성된 world model 안에서 RL policy를 마음껏 pretraining 시켜 sample efficiency를 극대화.
• Planning에 활용: TAMP(Task and Motion Planning)에서 영감을 받아, 1) 객체 간의 접촉을 기준으로 high-level abstract state space에서 큰 그림(경로)을 먼저 짜고, 2) 학습된 world model을 이용해 이를 실제 Atari 버튼 조작(low-level)으로 매핑하는 hierarchical planner 구현.

---

쉬운 설명 : 3 Modeling the World as a Product of Programmatic Experts (PoE-World)

이 섹션은 이 논문의 가장 핵심인 **"전문가 위원회 시스템"**이 구체적으로 어떻게 만들어지고 작동하는지 설명하는 파트입니다.

1. 어떻게 생겼는가? (Representation)

게임을 1명의 만물박사 AI가 통째로 예측하게 두는 게 아니라, 수백 명의 '단기 알바생(전문가)'들을 고용하는 것과 같습니다.

어떤 알바생은 "캐릭터가 오른쪽으로 갈 때의 속도"만 알고, 어떤 알바생은 "적과 부딪히면 죽는다"는 사실만 압니다. 플레이어가 어떤 행동을 하면, 이 알바생들이 각자 자기가 아는 지식을 바탕으로 다음 장면이 어떻게 될지 투표를 합니다. 이때 일 잘하는 알바생의 의견(높은 가중치)은 크게 반영하고, 엉뚱한 소리를 하는 알바생의 의견은 무시해서 최종 다음 장면을 예측합니다.

(단, "땅으로 꺼지면 안 된다" 같은 절대 원칙(Hard Constraints)을 하나 둬서 엉뚱한 예측이 나오는 것을 방지합니다.)

2. 어떻게 똑똑해지는가? (Learning)

처음 게임 영상을 조금 보여주고 LLM(챗GPT 같은 언어모델)에게 "규칙이 뭘까? 대충 파이썬 코드로 짧게 짧게 여러 개 짜봐"라고 시킵니다. 그러면 LLM이 수십 개의 코드(초기 알바생들)를 만들어냅니다.

이제 AI가 실제 게임을 플레이해보면서 이 코드들을 테스트합니다. 예측이 빗나가면 그 코드를 짠 알바생의 신뢰도 점수를 깎고, 예측이 잘 맞으면 점수를 올려줍니다. 점수가 너무 낮은 알바생은 해고(삭제)해버립니다. 이 과정을 반복하면 정말 쓸모 있고 정확한 규칙들만 남게 됩니다.

3. 어디에 써먹는가? (Usage)

이렇게 게임의 규칙을 완벽하게 이해한 '가상 세계(World Model)'가 완성되면, AI는 굳이 진짜 게임 화면에서 수만 번 죽어가며 배울 필요가 없습니다. 머릿속에 완벽한 시뮬레이터가 생겼으니 그 안에서 혼자 섀도우 복싱을 하며 게임 실력을 키울 수 있습니다(RL). 또한, "열쇠를 먹으려면 일단 사다리를 타야 해"라는 식의 큰 그림을 그리고 실행에 옮기는 치밀한 계획(Planning)을 세우는 데도 사용됩니다.

 

 

 

 

 

OCAtari가 좌표를 뽑고 행동은 에뮬레이터가 기록해뒀다.
OCAtari로 프레임을 object list(카테고리, bbox, velocity)로 변환한다.

준비되면 trajectory를 10-step batch 단위로 처리하면서,
t=0부터 10개 단위 구간마다 LLM에게 입력해서 코드를 생성시킨다
(왜 이렇게 변했냐는 가설을 먼저 세운 뒤 가설을 코드로 바꾸게 함).

LLM-based synthesis module은 총 10개이고,
각 모듈은 이동/충돌/생성/삭제/제약 등 서로 다른 측면에 집중하도록 설계되어 있다.

 

생성된 코드를 실행해 “다음 상태에 대한 제안값”을 얻고,

이를 피크+노이즈 형태의 분포로 바꾼 뒤 속성별로 관련 전문가들만 모아 PoE로 결합(곱)한다.

최종 분포에서 정답(next state)의 확률로 NLL loss를 계산하고, 이를 최소화하도록 전문가 가중치 θ를 함께 최적화한다.

최적화 후 θ<0.01인 전문가는 prune(삭제)한다.

새 데이터가 들어올 때마다 이 과정을 반복하면 Atari에 유효한 전문가 코드만 남는다.

 

 

별점 2.5점 / 5점

 

아이디어는 좋은데, OCAtari라는 보조 바퀴 없이는 못 달리는 자전거를 만든 것 같다. 실험도 너무 적어서 범용성을 믿을 수 없다.

 

월드의 규칙을 이해하는 작업을 매우 세밀한 code 단위로 나누어서 code 별로 가중치를 업데이트 하여 정확한 code만 남기게끔 하는 방법자체는 신선했음.