Diffusion : 논문 리뷰 : Locality in Image Diffusion Models Emerges from Data Statistics

용어 설명 (Glossary)

• Optimal Denoiser: 이론적으로 완벽하게 noise를 제거하는 함수. 하지만 실제로는 training set을 암기(memorization)해버려 새로운 이미지를 생성하지 못하는 "텔레포트" 현상을 보임.
• Inductive Bias: 모델이 학습하지 않은 데이터에 대해 예측할 때 사용하는 가정(assumption). 예: CNN은 이미지의 픽셀 간 지역적 상관관계(Locality)가 있다고 가정함.
• Locality: Denoising 과정에서 특정 픽셀의 값을 결정할 때, 입력 이미지의 해당 픽셀 주변(이웃) 정보만 주로 활용하는 성질.
• Sensitivity Field (Jacobian): 입력 이미지의 변화가 출력 이미지에 미치는 영향을 나타내는 map. 모델이 어디를 보고 복원을 수행하는지 시각화한 것.
• Wiener Filter: 데이터의 공분산(Covariance)과 SNR을 기반으로 noise를 제거하는 최적의 Linear Denoiser.
• Pass-through: 노이즈가 적은 상황(High SNR)에서 모델이 입력을 크게 바꾸지 않고 그대로 통과시키는 성질. Generalization의 핵심 요소로 간주됨.
• DiT (Diffusion Transformer): CNN 대신 Transformer 구조를 사용하는 Diffusion model. CNN과 달리 구조적으로 Global attention이 가능하여 Locality 강제성이 없음.

---

Purpose of the Paper

이 논문은 "Diffusion Model의 Generalization 능력은 어디서 오는가?" 에 대한 기존의 통념을 정면으로 반박하고 새로운 관점을 제시하기 위해 작성되었습니다.

• 기존 연구의 한계 (Problem): 기존 연구(Kamb & Ganguli 등)는 Deep Diffusion Model이 Generalization 할 수 있는 이유가 Neural Network Architecture(주로 CNN)의 Inductive Bias (Locality, Shift Equivariance) 때문이라고 주장했습니다. 즉, CNN 구조가 강제로 주변 픽셀만 보게 만들기 때문에 암기(memorization)를 피할 수 있다는 것입니다.
• 새로운 접근 방식 (Solution): 본 논문은 Locality가 아키텍처 때문이 아니라 Data Statistics(데이터 통계, 특히 공분산) 에서 자연스럽게 발생(Emerge)하는 현상임을 증명합니다.
• 연구의 핵심 목표: Deep Neural Network의 구조적 제약 없이도, 데이터 자체의 통계적 특성(Pixel Correlations)만으로 학습된 모델의 Locality 패턴이 결정됨을 보이고, 이를 통해 Linear Denoiser(Wiener Filter) 와의 연결고리를 확립하는 것입니다.

---

Key Contributions

이 논문은 Neural Network Architecture의 역할에 대한 과대평가를 경계하고, Data-Centric 관점에서 Diffusion Model의 동작 원리를 규명했습니다.

• Locality의 기원 규명 (Novel Finding):
  • Locality는 CNN의 Inductive bias가 아닌 Dataset Statistics에서 기인함을 입증했습니다.
  • 구조적으로 Global connection을 가진 Transformer (DiT) 도 CNN (U-Net)과 거의 동일한 Sensitivity Field를 학습한다는 것을 보여줌으로써, 아키텍처보다 데이터가 중요함을 증명했습니다.
• Linear Denoiser와의 연결성 (Theoretical Insight):
  • Deep Diffusion Model이 학습한 Sensitivity Field가 Optimal Linear Denoiser (Wiener Filter) 의 High-SNR Projection 연산자 형태와 놀라울 정도로 유사함을 발견했습니다.
  • 이는 복잡한 Neural Network가 사실상 데이터의 Principal Components(주성분) 중 SNR이 높은 성분만을 통과시키는(Pass-through) 방식으로 작동함을 시사합니다.
• Data Manipulation을 통한 검증 (Experimental Validation):
  • 데이터셋의 통계적 상관관계를 인위적으로 조작(예: "W" 모양의 correlation 추가)했을 때, 모델의 Sensitivity Field가 그 모양을 따라가는 것을 보여주며 가설을 강력하게 뒷받침했습니다.
• 새로운 Analytical Model 제안 (Methodological Contribution):
  • 기존처럼 모델의 Patch size를 측정해서 끼워 맞추는 방식이 아니라, 데이터의 통계(Wiener Filter) 로부터 직접 유도된 Analytical Denoiser를 제안했습니다. 이 모델은 기존의 복잡한 방법론들보다 실제 학습된 Diffusion Model의 동작을 더 정확하게 설명(High R2 score)합니다.

---

Experimental Highlights

이 논문은 다양한 데이터셋과 아키텍처 비교를 통해 가설을 검증했습니다.

• Sensitivity Field의 구조 비교:
  • CIFAR-10 (자연 이미지): Pixel 간 상관관계가 지역적이므로, U-Net, DiT, Wiener Filter 모두 Local & Isotropic 한 Sensitivity Field를 보임.
  • CelebA-HQ (정렬된 얼굴 이미지): 눈, 코, 입 등의 위치가 고정되어 있어 Pixel 간 상관관계가 전역적임. 이 경우 모델들은 Non-local, Location-dependent 한 패턴을 보임. (기존 Patch 기반 이론은 이를 설명 못함)
• Manipulated Dataset 실험:
  • CIFAR-10 데이터에 인위적인 "W" 형태의 상관관계를 주입하여 학습시킨 결과, Neural Network의 Sensitivity Field에 정확히 "W" 패턴이 나타남. 이는 Locality가 Learned Property from Data임을 명확히 보여주는 핵심 결과.
• Quantitative Benchmarks (R2 Score & MSE):
  • 제안된 Wiener Filter 기반 Analytical Model과 실제 학습된 DDPM 간의 예측 유사도를 측정.
  • CIFAR-10, CelebA-HQ, AFHQv2, MNIST 등 모든 데이터셋에서, 본 논문의 모델이 기존의 Kamb & Ganguli 모델(Patch-based)보다 월등히 높은 R2 Score와 낮은 MSE를 기록함.
  • 특히 Wiener Filter (Linear) 하나만으로도 기존의 복잡한 Analytical Model들을 능가하거나 대등한 성능을 보인다는 점이 충격적인 발견(Highlight).

---

Limitations and Future Work

• Limitations:
  • Linearity Assumption: 본 연구는 모델의 Sensitivity가 입력 이미지에 대해 상수(constant)라고 가정하는 Linear Regime에 집중했습니다. 하지만 Deep Neural Network는 본질적으로 Non-linear하므로, 이 가정이 깨지는 상황에 대한 분석이 부족합니다.
  • Second-order Statistics: Wiener Filter는 데이터의 평균과 공분산(2차 통계량)에만 의존합니다. 하지만 실제 이미지는 고차 통계량(Higher-order statistics)을 포함하고 있어, 이를 완벽히 설명하기엔 한계가 있습니다.
• Future Work:
  • Non-linear Regime 분석: Neural Diffuser의 비선형적 동작을 분석하여 생성 메커니즘을 더 깊이 이해하는 연구가 필요합니다.
  • Higher-order Statistics & Complex Architectures: 2차 통계량을 넘어선 고차 통계량과 더 복잡한 최신 아키텍처에서의 동작 원리를 규명하는 방향으로 확장되어야 합니다.

---

Overall Summary

이 논문은 Image Diffusion Model의 뛰어난 성능과 Generalization 능력이 특정 Neural Network Architecture(CNN 등)의 마법 같은 설계 때문이 아니라, 데이터 자체에 내재된 통계적 특성(Statistics) 을 모델이 충실히 학습한 결과임을 밝혀냈습니다. 저자들은 Deep Diffusion Model이 본질적으로 Optimal Linear Denoiser (Wiener Filter) 와 유사하게 High-SNR 신호를 보존(Pass-through) 하는 방식으로 작동함을 입증했습니다. 이는 Diffusion Model 연구의 초점을 '모델 구조 설계'에서 '데이터 통계 및 신호 처리적 관점'으로 전환시키는 중요한 이론적 토대를 마련했습니다.

---

쉬운 설명 (Simple Explanation)

우리는 흔히 "AI가 그림을 잘 그리는 건 뇌 구조(CNN 아키텍처)가 시야를 좁게(Locality) 쓰도록 설계되어서, 주변만 보고 그리기 때문이다"라고 생각했습니다.

하지만 이 논문은 이렇게 말합니다: "아닙니다. AI가 주변만 보고 그리는 건, 원래 데이터(사진) 자체가 주변 픽셀끼리만 비슷하기 때문입니다."

마치 사람 얼굴 데이터처럼 눈과 눈 사이가 멀어도 서로 관련이 있는 데이터를 주면, AI는 시야 제약 없이 멀리 떨어진 정보도 참조한다는 것을 증명했습니다. 결론적으로 복잡한 AI 모델도 알고 보니 "통계적으로 정보가 뚜렷한(SNR이 높은) 부분만 남기고 노이즈를 지우는 필터(Wiener Filter)" 와 거의 똑같이 작동하고 있었다는 것입니다.

 

 

 

 

Abstract

최근 연구는 image diffusion models의 generalization ability가 trained neural network의 locality properties에서 비롯된다는 것을 보여주었습니다. 특히, 특정 pixel을 denoising할 때, model은 해당 pixel 주변 input image의 제한된 neighborhood에 의존하며, 이전 연구에 따르면 이는 이 models가 novel images를 생성하는 능력과 밀접하게 관련되어 있습니다. Locality가 generalization의 핵심이기 때문에, diffusion models가 애초에 왜 local behavior를 학습하는지, 그리고 locality patterns의 속성을 지배하는 요인이 무엇인지 이해하는 것이 중요합니다.

본 연구에서는 deep diffusion models의 locality가 image dataset의 statistical property로 나타나는 것이며, 이전 연구에서 제안된 것처럼 convolutional neural networks의 inductive bias 때문이 아니라는 증거를 제시합니다. 구체적으로, 우리는 최적의 parametric linear denoiser가 deep neural denoisers와 유사한 locality properties를 보인다는 것을 입증합니다.

우리는 이론적으로나 실험적으로 이러한 locality가 image datasets에 존재하는 pixel correlations에서 직접 발생한다는 것을 보여줍니다. 게다가, locality patterns는 specialized datasets에서 급격히 다르며, data의 covariance에 대한 principal components에 근사합니다. 우리는 이러한 통찰력을 사용하여 이전의 expert-crafted alternatives보다 deep diffusion model에 의해 예측된 scores와 더 잘 일치하는 analytical denoiser를 제작합니다. 우리의 핵심 결론은 neural network architectures가 generation quality에 영향을 미치지만, 그들의 주요 역할은 data에 내재된 locality patterns를 포착하는 것이라는 점입니다.

 

 

1 Introduction

Denoising diffusion models는 generative modeling에서 state-of-the-art 결과를 달성했습니다. 특히 images, videos, audio와 같은 continuous data distributions를 포함하는 도메인에서 그렇습니다. 이들은 다양한 레벨의 Gaussian noise로 손상된 이미지로부터 clean image를 예측하도록 trained 됩니다. Diffusion model training objective에 대한 분석은 명백한 역설로 이어집니다: Objective는 training dataset의 함수일 뿐인 유일하고, analytical, non-parametric, closed-form solution을 허용합니다. 그러나, 이른바 optimal denoiser는 deep diffusion models의 outputs와 경험적으로 일치하지 않으며, 사실상 training set에 있는 images만 생성할 수 있어 완벽한 "memorization"을 보이고 novel images를 생성하는 데 실패합니다.

최근 연구는 이 역설을 조사하고 theory와 practice 사이의 간극을 좁히기 위해 optimal denoiser에 대한 변경을 제안합니다. Kamb와 Ganguli는 neural network architecture의 inductive biases—특히 convolutional neural networks의 shift equivariance와 locality biases—가 model이 loss function의 global optimum으로 수렴하는 것을 방지하여 generalization을 가능하게 한다고 가설을 세웁니다. 여기서 Locality는 denoising 동안, denoised output의 모든 pixel이 noisy input에 있는 해당 pixel 주변의 local neighborhood에만 민감하다는 것을 의미합니다. 그들은 closed-form optimal denoiser에 locality와 equivariance constraints를 추가하면 단순한 U-Net diffusion model이 생성한 것과 매우 유사한 images를 생성하는 model을 산출한다는 것을 입증합니다. 그러나 그들의 theory에는 핵심적인 한계가 있습니다: 기본 원리로부터 locality의 정도를 예측할 수 없다는 것입니다. 대신, 그들의 방법은 trained U-Net diffusion model의 receptive field를 측정하고 각 diffusion timestep에 대한 patch size를 추정한 다음 이를 analytical model의 parameter로 입력하는 데 의존합니다. 게다가, transformers와 같은 다른 neural network architectures도 유사하게 novel images를 생성할 수 있지만, 명시적인 locality나 shift-equivariance inductive biases가 부족합니다; 심지어 U-Nets도 일반적으로 전체 image를 커버하는 receptive field를 가집니다.

본 연구에서, 우리는 image diffusion models의 locality가 neural network architecture의 속성이 아니며, 대신 간단한 statistical analysis를 통해 training dataset에서 직접 도출될 수 있음을 입증합니다. 구체적으로, 우리는 data의 principal components—특히 그들의 signal-to-noise (SNR) ratio—를 분석하고, 서로 다른 architectures에 대해 학습된 sensitivity fields가 높은 SNR을 가진 principal components로의 projection operators에 근사함을 보여줍니다. Pixel 위치 전반에 걸쳐 높은 self-similarity를 가진 dataset인 CIFAR10에서는 단순한 locality pattern이 나타납니다. 그러나 중앙에 배치된 사람 얼굴 dataset인 CelebA-HQ에서는 sensitivities가 nonlocal하며, 예를 들어 눈과 같은 pixel 간의 correlations와 정렬됩니다. 우리는 이러한 동작을 Wiener filter라고 알려진 optimal linear denoiser와 연관시켜, diffusion models의 linear behavior를 관찰한 이전 연구와의 연결 고리를 확립합니다. 우리는 training set의 pixel statistics를 감지할 수 없을 정도로 편집함으로써 model의 sensitivity field에서 임의의 nonlocal patterns를 달성할 수 있음을 보여주어, sensitivity fields가 training set의 statistical properties와 일치하도록 학습된다는 추가 증거를 제공합니다.

우리는 trained deep diffusion model에 의한 generations와 얼마나 잘 일치하는지를 기준으로 최근 analytical models를 엄격하게 벤치마킹합니다. 놀랍게도, 우리는 간단한 Wiener filter가 optimal denoiser의 수정에 기반한 모든 최근 analytical methods보다 성능이 뛰어나다는 것을 발견했습니다. 그러나 우리의 analytically-derived sensitivity fields를 Kamb와 Ganguli의 model에 통합하면, CIFAR10, AFHQv2, CelebA-HQ를 포함한 여러 datasets에 걸쳐 현재까지 가장 성능이 좋은 analytical diffusion model을 산출합니다. 이 관찰은 dataset 전체의 pixel correlations를 포착하는 것이 denoising diffusion models의 성능에 주요한 역할을 한다는 증거를 제공합니다.

요약하면, 우리의 기여는 다음과 같습니다:

• 우리는 trained image diffusion models의 local sensitivities가 단지 model architecture의 inductive bias가 아니라 deep diffusion models의 학습된 속성임을 입증합니다.
• 우리는 optimal linear filter의 spatial sensitivity를 training data의 함수로서 분석적으로 도출하고, 이것이 denoising neural network에 의해 학습된 것과 밀접하게 일치하며, training data statistics에 따라 local 및 nonlocal sensitivities를 모두 산출함을 경험적으로 보여줍니다.
• 우리는 analytical diffusion model이 U-Net에 의해 만들어진 predictions를 얼마나 잘 설명하는지 측정하기 위한 정량적 벤치마크를 수립하고, 놀랍게도 이전의 optimal denoiser-based methods가 간단한 optimal linear filter보다 성능이 떨어진다는 것을 입증합니다.
• 우리는 analytically-computed locality를 Kamb와 Ganguli가 제안한 optimal denoiser-based model에 통합하고, 이것이 이전에 경험적으로 결정된 hyperparameter와 pre-trained neural networks에서 이를 측정해야 할 필요성을 제거하면서 대안적인 analytical models보다 성능이 뛰어남을 보여줍니다.

 

 

1 Introduction 정리노트 (for AI Researcher)

1. The Paradox of Denoising Diffusion Models

• Training Objective Analysis: Diffusion model training objective는 이론적으로 unique, closed-form solution인 optimal denoiser를 도출함.
• The Paradox: 이 이론상의 optimal denoiser는 training set을 완벽하게 memorization 할 뿐, novel images를 생성하지 못함. 반면, 실제 Deep Diffusion Models는 generalization에 성공함.

2. Previous Hypothesis & Limitations (Kamb & Ganguli [12])

• Hypothesis: Neural network architecture의 inductive biases(특히 CNN의 shift equivariance와 locality)가 model이 global optimum(memorization)에 빠지는 것을 막고 generalization을 유도한다고 주장.
• Method: Optimal denoiser에 locality와 equivariance constraints를 추가하여 U-Net과 유사한 결과를 얻음.
• Limitations:
  • Locality를 first principles(기본 원리)로부터 도출하지 못함.
  • Trained U-Net의 receptive field를 측정해 patch size를 추정하는 방식에 의존.
  • Explicit locality bias가 없는 Transformers나, 전체 이미지를 커버하는 receptive field를 가진 U-Net의 작동 원리를 설명하지 못함.

3. Core Contribution: Locality as a Statistical Property

• Main Claim: Locality는 architecture의 inductive bias가 아니라, training dataset의 statistical property(특히 Principal Components와 SNR)로부터 직접 도출되는 것임.
• Evidence:
  • CIFAR10 (High self-similarity): Simple locality pattern이 나타남.
  • CelebA-HQ (Centered human faces): Eyes 간의 관계 등 nonlocal correlation과 정렬된 sensitivity를 보임.
  • Pixel Statistics Editing: Training set의 pixel statistics를 미세하게 수정하면 model의 sensitivity field를 임의의 nonlocal pattern으로 바꿀 수 있음.
• Connection to Linear Models: Learned sensitivity fields는 high SNR을 가진 Principal Components로의 projection operators에 근사하며, 이는 **optimal linear denoiser (Wiener filter)**와 연관됨.

4. Benchmarks & Results

• Surprising Finding: 단순한 Wiener filter가 기존의 복잡한 optimal denoiser 기반 수정 방법들보다 Deep Diffusion Model의 generation과 더 잘 일치함.
• SOTA Achievement: 본 논문에서 분석적으로 도출한(analytically-derived) sensitivity fields를 Kamb & Ganguli의 model에 통합한 결과, CIFAR10, AFHQv2, CelebA-HQ에서 가장 우수한 성능을 달성.
• Conclusion: Neural network architectures가 generation quality에 영향을 주긴 하지만, 그들의 주된 역할은 data에 내재된 locality patterns (pixel correlations)를 포착하는 것임.

---

쉬운 설명 :

"AI가 그림을 잘 그리는 이유는 붓(모델 구조) 때문일까, 그림 대상(데이터) 때문일까?"

1. 기존의 미스터리: 수학적으로 완벽하게 계산된 '최적의 제거기(Optimal Denoiser)'는 훈련된 이미지를 앵무새처럼 외우기만 하고 새로운 그림을 못 그립니다. 그런데 실제 AI 모델(딥러닝)은 새로운 그림을 잘 그려냅니다. 왜 그럴까요?
2. 기존 학설 (도구 탓): AI 모델이 사용하는 구조(CNN 등)가 한 번에 좁은 영역만 볼 수 있는 한계(Locality)가 있어서, 억지로 전체를 외우지 못하게 되니 오히려 창의력(일반화)이 생긴 것이라고 믿었습니다.
3. 이 논문의 발견 (데이터 탓): "아니다, 구조 때문이 아니다." 연구진이 분석해보니, AI가 좁은 영역을 보는 성질(Locality)은 데이터 자체의 통계적 특성 때문에 생기는 것이었습니다.
   • 예를 들어, 풍경 사진(CIFAR10)은 좁은 영역끼리 연관성이 높아서 좁게 보는 것이고, 사람 얼굴(CelebA-HQ)은 왼쪽 눈과 오른쪽 눈처럼 멀리 떨어진 픽셀끼리도 연관성이 있어서 AI가 이를 파악해 멀리까지 본다는 것입니다.
4. 결론: AI 모델의 구조가 훌륭해서가 아니라, AI가 **데이터 속에 숨겨진 픽셀 간의 상관관계(통계)**를 아주 잘 파악했기 때문에 그림을 잘 그리는 것입니다. 실제로 연구진이 복잡한 딥러닝 없이 통계적 원리만 적용한 간단한 필터(Wiener filter)를 써봤더니, 기존의 복잡한 이론 모델보다 훨씬 더 실제 AI와 비슷한 결과를 냈습니다.

2 Preliminaries and Related Work

우리는 우리의 주된 탐구 라인인 deep diffusion networks의 analytical models 구축을 위한 예비 지식과 관련 연구를 논의합니다.

Denoising diffusion models. Score-based image generative models [8, 27, 28]은 clean data에 Gaussian noise를 추가하는 과정을 역으로 수행하는 것을 학습합니다. Training 동안, 우리는 training data distribution $X$에서 data point $x_0$, 구간 $[0, 1]$에서 noise level $t$, 그리고 Gaussian noise direction $\epsilon \sim \mathcal{N}(0, I)$를 샘플링합니다; noise schedule $\alpha_t$는 $\alpha_0 = 1$이고 $\alpha_1 = 0$이 되도록 선택됩니다. 그런 다음 우리는 $x_t = \sqrt{\alpha_t}x_0 + \sqrt{1 - \alpha_t}\epsilon$를 얻기 위해 $x_0$에 noise를 추가합니다. Image diffusion model $f(x, t)$에 대한 training objective는 score-matching으로도 알려져 있으며, $x_t$가 주어졌을 때 $x_0$를 예측하는 것을 목표로 합니다:

$$\min_f \mathbb{E}_{x_0 \sim X, \epsilon \sim \mathcal{N}(0, I), t \sim [0, 1]} \left\| f(\sqrt{\alpha_t}x_0 + \sqrt{1 - \alpha_t}\epsilon, t) - x_0 \right\|^2_2 \quad (1)$$

최근 연구들은 diffusion models의 generalization capabilities를 탐구하여, 이론적인 memorization 성향과 경험적인 novel samples 생성 능력 사이의 모순을 강조했습니다. Yoon et al. [34]은 memorization-generalization 이분법을 소개하며, diffusion models가 training data를 memorizing하는 것을 피할 때 generalize한다고 가정합니다. Yi et al. [33]은 mutual information metrics를 통해 generalization을 공식화하여, trained diffusion models가 경험적인 optimal solutions를 넘어 generalize할 수 있음을 입증했습니다. Gu et al. [7]은 이 현상을 더 조사하여, dataset size와 conditioning과 같은 요인이 diffusion models의 memorization 정도에 영향을 미칠 수 있음을 밝혔습니다.

Analytical diffusion via the optimal denoiser. 여러 연구들 [5, 14, 23, 25]은 optimal denoiser를 deep diffusion models의 행동에 대한 유망한 analytical model로 식별합니다. (1)을 최소화하는 이 optimal denoiser $\hat{f}(x, t)$는 conditional expectation으로 쓸 수 있습니다:

$$\hat{f}(x, t) = \mathbb{E}[x_0 | x_t = x] \quad (2)$$

Data distribution이 유한한 empirical distribution $X = {x^{(i)}0}{i \in [N]}$으로 근사될 때, 그리고 density $p(x_t) = \mathcal{N}(\sqrt{\alpha_t}x_0, (1 - \alpha_t)I)$에 대한 analytic form을 가지고 있다는 사실 때문에, optimal denoiser는 closed-form으로 사용 가능합니다 [5, 14, 23, 25]:

$$\hat{f}(x, t) = \sum_{i=1}^N w_i(x, t)x^{(i)}_0, \quad w_i(x, t) = \text{softmax}_i \left( -\frac{1}{2\sigma^2_t} \left\| \frac{1}{\sqrt{\alpha_t}} x - x^{(j)}_0 \right\|^2 \right)_{j \in [N]}, \quad (3)$$

여기서 $\sigma^2_t = (1 - \alpha_t)/\alpha_t$이고 $\text{softmax}i {a_j}{j \in [N]} = \frac{\exp(a_i)}{\sum_{j=1}^N \exp(a_j)}$입니다. 이것은 optimal denoiser를 training set에 대한 kernel-weighted average로 표현하며, deep neural networks에 대한 적절한 model로서 optimal denoiser의 핵심적인 한계를 명확히 합니다: noise level이 0에 가까워짐에 따라, softmax 항은 사실상 training set에서 nearest neighbor를 선택합니다. 결과적으로, optimal denoiser는 항상 training set에 있는 image를 생성하고 결코 novel image를 생성하지 않습니다.

Improving the optimal denoiser via smoothing. Generalization을 촉진하기 위해, Scarvelis et al. [25]은 score function을 smoothing하여 training data와 다른 novel samples를 생성할 것을 제안합니다. Niedoba et al. [18]은 analytical score models의 구현을 지원하기 위해 효율적인 nearest neighbor search를 도출합니다. 별도로, Shah et al. [26]은 small-data regime에서 neural network models가 generalize하도록 장려하기 위해 Gaussian noise를 추가하여 empirical training data distribution을 smoothing할 것을 제안합니다. Aithal et al. [1]은 diffusion models의 hallucinations가 data distribution의 modes 사이의 smooth interpolation 때문에 발생한다고 주장합니다. 그러나 단순히 score function을 smoothing하는 것은 training images 간의 pixel-space interpolation으로 이어지며, 실제로 관찰되는 고품질의 선명한 novel images를 설명하지 못합니다.

Adding inductive biases to the optimal denoiser. Kadkhodaie et al. [11]은 neural networks의 inductive biases가 data density와 잘 맞아떨어져서, 효과적으로 data를 image structure에 적합한 low-dimensional basis로 투영한다는 것을 관찰했습니다. 이 통찰력을 바탕으로, Kamb와 Ganguli [12] 및 Niedoba et al. [19]은 optimal denoiser와 deep diffusion models 사이의 간극이 denoiser를 근사하는 데 사용되는 deep neural network의 inductive bias에서 비롯된다고 제안합니다. 구체적으로, 그들은 convolutional U-Net [24]의 구조가 score-matching objective 식 (1)의 함수 $f$에 locality 및/또는 shift equivariance의 constraints를 부과한다고 가정합니다:

$$\min_f \mathbb{E}_{x_0 \sim X, \epsilon \sim \mathcal{N}(0, I), t \sim [0, 1]} \|f(\sqrt{\alpha_t}x_0 + \sqrt{1 - \alpha_t}\epsilon, t) - x_0\|^2_2 \quad (4)$$

$$\text{s.t. } f_q(x, t) = f_q(M^q_t x, t) \quad \forall q \in [Q] \quad (\text{locality})$$

$$f(g \circ x, t) = g \circ f(x, t) \quad \forall g \in T(2), \quad (\text{equivariance})$$

여기서 $f_q$는 output의 pixel $q$ (총 $Q$ pixels 중)이고, $M^q_t$는 각 time-step $t$에 대해 pixel $q$ 주변의 patch를 선택하는 masking operator이며, $T(2)$는 $\circ$를 통해 $x \in \mathbb{R}^n$에 작용하는 2D translation group입니다. 그들은 일반적인 $M^q_t$에 대해, constrained score-matching objective 식 (4)의 해가 식 (3)과 유사한 형태를 가지지만, 각 pixel $q$에 특정한 가중치를 갖는다는 것을 보여줍니다:

$$\hat{f}_q(x, t) = \sum_{i \in [N], g \in T(2)} w^q_{i, g}(x, t)(g \circ x^{(i)}_0)_q, \quad w^q_{i, g}(x, t) = \text{softmax}_{i, g} \left( -\frac{1}{2\sigma^2_t} \left\| M^q_t \left( \frac{1}{\sqrt{\alpha_t}} x - h \circ x^{(j)}_0 \right) \right\|^2_2 \right)_{j \in [N], h \in T(2)}, \quad (5)$$

여기서 $M^q_t$는 binary mask이며, 우리는 다시 mask에 의해 정의된 subspace로 투영된 isotropic multivariate Gaussian으로 귀결됩니다. 효과적으로, 이 model은 각 training image를 $M_t$ 크기의 patches로 나누고, 그들의 위치를 잊어버리고 (equivariance), $q$를 중심으로 하는 patch로부터의 거리에 따라 가중된 ground truth patches의 center pixels 평균을 취하여 각 input pixel을 denoises합니다. Kamb와 Ganguli [12]는 가능한 모든 square binary patches를 반복하고 trained diffusion model과 가장 좋은 correlation을 산출하는 것을 선택하여 각 noise level $t$에 대한 patches를 얻습니다. Niedoba et al. [19]은 patches의 모양에 대한 constraint를 완화하여 임의의 모양일 수 있지만 compact하고 모든 pixels에 걸쳐 평균화되도록 허용합니다. 그런 다음 그들은 trained U-Net의 average sensitivity를 측정하고 이를 binarize하여 masks를 얻습니다. 두 연구 모두 mask $M^q_t$를 trained models의 경험적으로 관찰된 locality fields에 맞추고 각 pixel $q$에 대한 모든 masks를 평균화합니다. 즉, $M^q_t$와 $M^p_t$는 translation까지 동일합니다.

Linear denoisers. 최근 연구들은 diffusion models가 강력한 linear behavior를 보인다는 것을 밝혀냈습니다. Wang과 Vastola [29, 30]는 높은 noise levels에서 well-trained diffusion models의 학습된 score functions가 linear models의 것들과 밀접하게 일치한다는 이론적 및 경험적 증거를 제공합니다. Linear denoisers는 잘 연구되어 있으며 [2, 20, 31], linear로 제한된 optimal denoiser가 Gaussian dataset [15]에 대한 optimal denoiser와 동일한 형태를 갖는다는 것을 보일 수 있습니다. Li et al. [17]은 특히 generalization regime과 높은 수준의 noise diffusion에 대해, denoisers가 dataset의 empirical mean과 covariance로 특성화되는 multivariate Gaussian distribution에 대한 optimal denoiser에 근사한다는 것을 입증합니다.

 

 

 

2 Preliminaries and Related Work 정리노트 (for AI Researcher)

1. The "Optimal Denoiser" Trap (Theoretical Paradox)

• Definition: Diffusion objective(Eq. 1)의 이론적 해(Solution)는 $X$가 유한한 empirical distribution일 때, Closed-form Analytical Solution(Eq. 3)을 가짐.
• $$\hat{f}(x, t) = \sum_{i=1}^N w_i(x, t)x^{(i)}_0$$
• Mechanism: Training set에 대한 Kernel-weighted average 형태.
• Critical Issue: Noise level $t \to 0$일 때, softmax term이 가장 가까운 training sample 하나에만 집중(Peaked)하게 됨.
  • $\therefore$ Perfect Memorization: 이론상 최적의 denoiser는 Nearest Neighbor와 동일하게 작동하며, Novel Image를 절대 생성하지 못함.

2. Existing Attempts to induce Generalization

• Smoothing Approaches: Score function이나 Data distribution을 스무딩하여 generalization을 유도하려 했으나, 이는 Training images 간의 Pixel-space interpolation을 초래하여, 실제 Diffusion model이 보여주는 선명한(sharp) 고품질 이미지 생성 원리를 설명하지 못함.

3. The Direct Predecessor: Inductive Bias Constraints (Kamb & Ganguli [12])

• Hypothesis: Deep Diffusion Model과 Optimal Denoiser 간의 간극은 Neural Network(U-Net)의 Inductive Bias(Locality & Shift Equivariance) 때문이라고 가정.
• Methodology: Optimal Denoiser 수식에 **Masking Operator $M^q_t$**를 도입하여 강제로 Locality 제약 조건을 부과 (Eq. 5).
• $$\hat{f}_q(x, t) = \sum_{i, g} w^q_{i, g}(x, t)(g \circ x^{(i)}_0)_q$$
• Mechanism: 이미지를 Patch 단위로 쪼개고 위치 정보(Global location)를 무시한 채, Patch 간의 유사도를 기반으로 Denoising 수행. (Patch-mixing을 통한 Generalization 유도)
• Limitations (Target of this paper): Mask $M^q_t$를 결정하기 위해 Trained U-Net의 Receptive field를 측정하거나 Heuristic search를 사용해야 함. 또한, 모든 픽셀에 대해 동일한 모양의 Mask(Translation Invariant)를 가정함.

4. Linear Denoisers (Connection to Gaussian)

• Observation: High noise level에서 Diffusion model은 Linear Model과 매우 유사하게 동작함.
• Theoretical Link: Linear constrained optimal denoiser는 Multivariate Gaussian distribution에 대한 Optimal denoiser와 동일한 형태를 가짐.
• Significance: 본 논문이 뒤이어 제안할 "Simple Wiener Filter(Linear)"가 복잡한 모델보다 우수할 수 있다는 배경지식을 제공.

---

쉬운 설명 :

"수학적으로 완벽한 정답 vs. 인간처럼 그리는 AI"

1. 완벽함의 함정 (Optimal Denoiser):
2. 수학공식으로 완벽하게 계산된 '최적의 복원기'는 융통성이 전혀 없습니다. 노이즈가 낀 이미지를 주면, 훈련 데이터 중에서 가장 비슷한 원본 사진을 그대로 찾아내기만(Memorization) 합니다. 즉, 새로운 그림을 창조하는 능력은 0점입니다.
3. 기존 연구자들의 해결책 "시야를 가리자" (Kamb & Ganguli):연구자들은 AI 모델(U-Net)의 구조적 특징 때문에 AI가 전체를 보지 못하고 **'좁은 영역(Patch)'만 본다(Locality)**고 생각했습니다. 그래서 수학 공식에도 강제로 **"한 번에 좁은 구멍으로만 봐!"**라는 제약을 걸었습니다. 그랬더니 AI가 전체를 베끼지 못하고, 여기저기서 조각(Patch)을 가져와 이어 붙이면서 새로운 그림을 만들어내기 시작했습니다.
4. "AI가 훈련 데이터를 통째로 외우지 못하게 하려면 어떻게 해야 할까?"
5. 한계점:
6. 하지만 이 방법은 "얼마나 좁게 봐야 하는지", "어떤 모양으로 봐야 하는지"를 알아내기 위해, 이미 다 학습된 AI 모델을 뜯어보거나 주먹구구식으로 찾아야 했습니다. (이 논문은 이 부분을 지적하며, 데이터만 있으면 통계적으로 바로 알 수 있다고 주장할 예정입니다.)

 

 

 

 

3 Deriving Denoising Sensitivity from Dataset Statistics

이 섹션에서는 patch-based optimal denoisers [12, 19]에서 generalization과 locality 사이의 관계를 탐구하고 이를 diffusion models에서 관찰된 linearity [17, 29, 30]와 연결합니다. 식 (3)의 optimal denoiser와 달리, trained diffusion models는 높은 signal-to-noise (SNR) ratio data 방향을 따라 input information을 유지하는 “pass-through” behavior를 보입니다. 우리는 patch-based optimal denoisers에서 locality를 제한함으로써, 이전 연구들이 효과적으로 linear denoisers의 “pass-through” behavior를 채택하여 novel images를 생성할 수 있게 되었다고 가정합니다.

Sampling voids. Optimal denoiser $\hat{f}(x, t)$는 모든 $x \in \mathbb{R}^n$ 및 $t \in (0, 1)$ 값에 대해 잘 정의되어 있지만, neural network denoiser가 훈련되는 $(x_t, t)$의 distribution은 training process 전체에 걸쳐 드물게 샘플링될 low-density regions를 가지고 있습니다. 예를 들어, $t \to 0$ (low noise regime)일 때, training data에서 멀리 떨어진 $\mathbb{R}^n$ 영역은 식 (1)의 score-matching objective로 diffusion model을 훈련할 때 과소 샘플링될 것입니다. 이는 Figure 1 (왼쪽)에 설명되어 있으며, test images 근처의 작은 noise 영역은 어떠한 training samples로도 덮이지 않습니다. 우리는 식 (1)의 empirical samples로 덮이지 않는 $\mathbb{R}^n \times [0, 1]$의 부분을 sampling void regions라고 부를 것입니다. 한편으로, 이러한 regions에서 denoiser의 behavior는 generalization에 중요합니다. 다른 한편으로, training 동안 공간의 이 부분에 empirical samples가 없었기 때문에, optimal denoiser는 이러한 regions에서 trained diffusion model의 좋은 model이 아닙니다. 다음 섹션들에서 우리는 sampling void regions에서 trained diffusion models의 behavior에 대해 추론하는 방법에 대한 직관을 구축할 것입니다.

“Pass-through” denoisers. 식 (3)의 optimal denoiser가 training dataset 밖의 test image와 함께 제공되고 noise의 양이 작을 때, softmax는 더 선택적으로 변하며, optimal denoiser는 $x_0$를 dataset에서 가장 가까운 image로 예측할 것입니다 (Figure 1, 중간 참조). 이러한 behavior는 generalization을 방지하는데, $\sigma_t \to 0$일 때 모든 novel image가 training dataset의 가장 가까운 이웃으로 “teleported”될 것이기 때문입니다.

Figure 1의 관찰에서 영감을 받아, 우리는 denoisers의 “pass-through” properties에 대한 직관을 개발합니다. 작은 noise levels에 대해, image의 많은 정보는 추가된 noise에 의해 파괴되지 않습니다. Optimal denoiser와 달리 “좋은” denoiser는 $x_0$ 추정에서 이 정보를 유지할 것이라고 가정하는 것이 자연스럽습니다. $x_t$의 어떤 부분이 적은 양의 noise에 의해 영향을 받지 않을까요? 비공식적으로, natural images의 경우, 적은 양의 noise를 추가한 후에도 low frequencies가 “생존”합니다. 우리는 1) noise를 추가하는 것이 data의 상위 principal components를 보존하고, 2) 이러한 principal components가 natural images의 low-frequency features에 해당한다는 것을 관찰함으로써 이 직관을 공식화합니다. Data의 principal components는 covariance matrix $\text{Cov}(X) = U\text{diag}(\lambda^2_1, \lambda^2_2, \dots, \lambda^2_N)U^T$의 eigendecomposition에서 나오며, 여기서 $U$는 eigenvectors의 행렬이고 $\lambda^2_i$는 eigenvalues입니다. Noise의 covariance matrix $\sigma^2_t I$ 또한 이 basis에서 isotropic하므로, $i$-th principal component를 따른 signal-to-noise ratio (SNR)는 $\lambda^2_i / \sigma^2_t$입니다. 고전적인 image processing 문헌 [10]에서 natural images의 경우 이 eigenbasis가 Fourier basis에 근사하며, 따라서 가장 높은 variance components (즉, high SNR)가 low-frequency features에 해당한다는 것은 잘 알려져 있습니다. 따라서 직관적으로, “pass-through” projection은 low-pass filter와 유사합니다. 그러나 일반적으로는 그렇지 않으며, 더 구체적인 datasets의 경우 “pass-through” projection은 단순히 low-pass filter가 아닙니다. 예를 들어, 섹션 4에서 보여주겠지만, 중앙에 배치되고 정규화된 사람 얼굴 (즉, Celeba-HQ/FFHQ)과 같은 datasets의 경우, eigen-basis는 Fourier basis와 매우 다르며, 따라서 trained denoisers에서 관찰된 locality patterns는 translation equivariant하지도 않고 isotropic하지도 않습니다.

Connection to Gaussian data and linear denoiser. 이전 문단들의 직관은 dataset이 단일 covariance matrix로 잘 설명된다는 가정 (Gaussian data distribution을 가정) 위에 구축되었습니다. 이 경우, input noise images를 high-SNR principal components로 단순히 투영함으로써 간단한 denoiser를 제작할 수 있습니다:

$$W_t = \frac{1}{\sqrt{\alpha_t}} U\text{diag} \left( \frac{\lambda^2_i}{\lambda^2_i + \sigma^2_t} \right) U^T. \quad (6)$$

Gaussian dataset 가정 $x_0 \sim \mathcal{N}(0, \Sigma)$ [15] 하에서 optimal인 이 denoiser는 Wiener filter [31]로 알려져 있습니다. 동시에, Wiener filter는 linear constraint $f(x_t) = A_tx_t$ [31] 하에서 식 (1)을 최소화하는 optimal linear denoiser이기도 합니다. 식 (6)에서 볼 수 있듯이, 이는 input을 data의 principal components로 투영하고, 그들의 SNR에 따라 이러한 projections를 축소하며, 다시 data space로 투영합니다. 여러 이전 연구들 [17, 29]에서 보고된 바와 같이, trained diffusion models는 linear behavior를 보이며 놀라울 정도로 Wiener filter로 잘 근사될 수 있습니다. 본 연구의 뒷부분에서, 우리는 이러한 관찰을 확장하여 Wiener filter가 기존의 patch-based analytical denoisers [12, 18]와 동등하거나 더 나은 성능을 발휘함을 입증합니다.

Locality and sensitivity. 지금까지 우리는 “좋은” denoiser가 sampling void regions—optimal denoiser analysis가 더 이상 효과적이지 않지만 generalization에 중요한 공간의 부분들—에서 input의 high-SNR components를 “pass-through”해야 한다는 직관을 구축했습니다. [12, 19]에 따르면, denoisers의 sensitivity fields의 locality는 generalization에 중요한 역할을 합니다. 하지만 이것이 위의 “pass-through” 직관과 어떻게 관련될까요?

그 관계를 보여주기 위해, 우리는 locality의 개념으로 돌아갑니다. Locality란 neural network의 제한되고 일반적으로 compact sensitivity field를 의미합니다. 공식적으로, denoiser $f(x, t)$의 sensitivity field는 input–output Jacobian $S_f(x, t) = \partial f(x, t)/\partial x$입니다. Kamb와 Ganguli [12]는 diffusion models의 학습된 locality patterns를 square patches로 근사하며, 이것들이 compact하고 대략 isotropic하며 output pixel 위치와 input image 모두에 대해 일정하다고 가정합니다. 섹션 4에서 입증하겠지만, 이러한 가정 중 어느 것도 보편적이지 않으며, 다양한 natural images datasets에 대해서는 합리적이지만, 더 specialized datasets에 대한 neural diffusers의 sensitivities는 위의 가정 중 어느 것이든 위반할 수 있습니다.

우리의 분석을 위해, 우리는 input image $x$에 대한 model의 sensitivity field의 독립성 가정을 유지하고 다른 모든 가정을 해제하여, locality patterns가 임의의 모양을 취하고 output pixel에 의존하도록 허용합니다. Sensitivity $S_f(x, t)$가 $x$에 대해 일정하다는 가정 하에, denoiser는 $x$에서 linear하며 $f(x, t) = A_t x + B_t$ 형태를 취합니다. 여기서 $A_t$는 sensitivity이고 $B_t$는 bias term입니다. Linear constraint 하에서 식 (1)의 해는 Wiener filter이며, 따라서 dataset이 중앙에 있다고 가정할 때 $A_t = W_t$이고 $B_t = 0$임을 상기하십시오. 각각의 개별 output pixel $q$에 대해, sensitivity는 다음과 같

 

 

이 이미지는 논문의 핵심 주장인 **"Optimal Denoiser의 한계와 Deep Diffusion Model(U-Net)의 차이"**를 시각적, 정량적으로 보여주는 매우 중요한 Figure입니다. 세 부분으로 나누어 설명해 드리겠습니다.

Figure 1 분석

1. Left: Sampling Voids (학습되지 않은 공간)

• 개념 시각화: $x$축은 spatial dimension, $t$축은 noise level을 나타냅니다.
• Training Cones: $x_0^{(1)}$과 $x_0^{(2)}$는 training data points입니다. Noise가 추가됨에 따라($t$가 커짐에 따라), 이 데이터들이 분포하는 영역(파란색/빨간색 선 안쪽)은 **"high-probability-density cones"**를 형성합니다.
• Sampling Void: 새로운 test point $x_0^{(\text{test})}$(분홍색 점)에 적은 양의 noise $t'$이 추가되었을 때, 그 지점 $x_{t'}^{(\text{test})}$는 어떠한 training cones에도 속하지 않는 빈 공간(Sampling Void)에 위치하게 됩니다.
• 의미: Model은 학습 중에 이 void 영역을 본 적이 없습니다. 따라서 이 영역에서의 denoiser 동작은 정의되지 않았으며(undefined), 여기서 어떻게 동작하느냐가 generalization을 결정합니다.

2. Middle: Visual Comparison (시각적 비교)

• Row 1 (Top): $x_0^{(\text{test})}$ (Clean Test Images). 개구리, 자동차, 새 등.
• Row 2: $x_{t'}$ (Noisy Input). 적은 양의 noise가 추가된 상태.
• Row 3 ($f_\theta$): **Trained Diffusion Model (U-Net)**의 결과. Input image의 대략적인 구조(coarse structure)를 **"pass-through"**하여 원본과 시각적으로 유사한 이미지를 복원합니다. (Generalization 성공)
• Row 4 ($f^*$): Optimal Denoiser의 결과. Input과 비슷해 보이는 training set의 이미지로 **"teleports"**해버립니다. 예를 들어, 첫 번째 열의 개구리가 다른 모습의 개구리로 바뀌거나, 배경이 완전히 달라집니다. (Memorization 발생, Generalization 실패)

3. Right: MSE Analysis (정량적 분석)

• X축: Noise level $\sigma$.
• Y축: 원본 $x_0$에 대한 MSE (Mean Squared Error).
• Blue Line (U-Net): Low noise level(왼쪽)에서 MSE가 매우 낮습니다. 즉, 원본 $x_0^{(\text{test})}$를 잘 보존합니다.
• Orange Line (Optimal): Low noise level에서도 MSE가 높게 유지됩니다. 이는 Optimal Denoiser가 $x_0^{(\text{test})}$가 아닌 엉뚱한 training data $x_0^{(train)}$을 예측하기 때문입니다.
• Convergence: Noise가 매우 커지면(오른쪽), 두 모델의 동작이 비슷해지며 수렴합니다.

---

핵심 요약

이 Figure는 **"수학적으로 완벽한 Optimal Denoiser"**가 실제로는 Low Noise Regime에서 가장 가까운 훈련 데이터를 찾아가는 Nearest Neighbor Search처럼 동작하여 Memorization에 빠진다는 것을 증명합니다.

반면, **Deep Diffusion Model (U-Net)**은 학습하지 않은 영역(Sampling Void)에서도 입력 이미지의 구조를 유지(Pass-through)하는 특성이 있어 Generalization이 가능하다는 것을 보여줍니다. 논문은 이러한 U-Net의 특성이 Architecture 덕분이 아니라 **Data Statistics(Locality)**를 학습했기 때문이라고 주장합니다.

 

 

3 Deriving Denoising Sensitivity from Dataset Statistics 정리노트 (for AI Researcher)

1. The "Sampling Voids" Problem & Generalization

• Issue: Optimal Denoiser $\hat{f}(x, t)$는 모든 영역에서 정의되지만, 실제 학습 데이터 분포는 고차원 공간에서 매우 희소함(Low-density regions).
• Sampling Voids: $t \to 0$ (Low noise regime)일 때, Test sample 주변 영역은 Training process에서 전혀 샘플링되지 않은 "공백(Voids)" 상태임 (Fig 1 참조).
• Behavior Divergence:
  • Optimal Denoiser: 이 영역에서 Softmax가 Peaked되어 가장 가까운 Training sample로 **"Teleport"**함 (Memorization).
  • Trained Model: Input의 정보를 보존하며 "Pass-through" 함 (Generalization).

2. "Pass-through" Property & PCA

• Intuition: "Good" denoiser는 노이즈에 의해 파괴되지 않은 정보를 그대로 통과시켜야 함.
• Signal Analysis:
  • Small noise에서 살아남는 정보 = High Principal Components (PCs) of Data Covariance.
  • Noise는 Isotropic하므로, $i$-th PC의 SNR은 $\lambda_i^2 / \sigma_t^2$로 결정됨.
• Natural Image vs. Specialized Data:
  • 자연 이미지: Eigenbasis $\approx$ Fourier basis (Low-freq = High SNR). 따라서 Low-pass filter처럼 동작.
  • 특화 데이터(Face 등): Eigenbasis가 Fourier와 다름. 따라서 단순 Low-pass가 아님.

3. Connection to Wiener Filter (Linear Denoiser)

• 데이터 분포를 Single Gaussian으로 가정할 경우 ($x_0 \sim \mathcal{N}(0, \Sigma)$), Optimal Denoiser는 Wiener Filter가 됨.
• $$W_t = \frac{1}{\sqrt{\alpha_t}} U \text{diag} \left( \frac{\lambda^2_i}{\lambda^2_i + \sigma^2_t} \right) U^T$$
• Mechanism: Input을 PC로 투영 $\to$ SNR에 따라 Shrinkage $\to$ 다시 복원.
• Significance: Deep Diffusion Model은 High noise 및 Early training 단계에서 이 Linear behavior(Wiener filter)를 매우 잘 근사함.

4. The Origin of Locality (Key Contribution)

• Refuting Previous Assumptions: 기존 연구([12, 19])는 Locality를 Architecture(CNN)의 Inductive Bias로 보았으나, 본 논문은 이를 Data Statistics의 결과로 해석.
• Derivation from Linearity: Denoiser가 $x$에 대해 Linear하다면 ($S_f(x, t) \approx A_t$), Sensitivity Matrix는 Wiener Filter $W_t$와 같아짐.
• $$S^q_f(x, t) = \left[ U \text{diag} \left( \frac{\text{SNR}_i}{\text{SNR}_i + 1} \right) U^T \right]_q$$
• Mathematical Proof of Locality:
  • $\sigma_t \to 0$ (Low noise) $\Rightarrow$ $\text{SNR} \to \infty$
  • $\Rightarrow$ $S^q_f \to 1_q$ (Identity / Indicator function)
  • 즉, 노이즈가 줄어들수록 Sensitivity Field는 수학적으로 필연적으로 좁아짐(Shrink).
• Conclusion: Sensitivity field의 형태(Locality, Shape)는 Model Architecture가 아니라 Data Covariance ($U$)와 SNR에 의해 결정됨. 데이터가 Local correlation을 가지면 Model도 Local해지고, Non-local(예: 눈과 눈 사이)하면 Model도 Non-local해짐.

---

쉬운 설명 :

"AI가 '좁게 보는 능력(Locality)'은 어디서 왔을까?"

1. 멍청한 천재 (Optimal Denoiser): 수학적으로 완벽한 공식은 융통성이 없습니다. 노이즈가 조금만 낀 새로운 사진을 주면, 자기가 아는 족보(훈련 데이터) 중에서 가장 비슷한 사진을 찾아서 그걸로 순간이동(Teleport) 시켜버립니다. 즉, 새로운 걸 못 만듭니다.
2. 현명한 필터 (Pass-through): 반면, 똑똑한 모델은 노이즈 속에서도 "살아남은 뼈대(강한 신호)"를 알아봅니다. 이 뼈대는 데이터 통계학적으로 **주성분(Principal Components)**이라고 부릅니다.
3. 핵심 반전: 기존에는 AI 모델이 "원래 좁게 보는 구조(CNN)"라서 주변 픽셀만 보고 복원한다고 생각했습니다. 하지만 수식을 풀어보니 그게 아니었습니다.
   • 데이터의 통계적 특성상, 노이즈가 적을수록 "그냥 자기 자신(해당 픽셀)을 믿는 것"이 정답에 가까워집니다.
   • 즉, AI가 좁은 영역만 보는 건(Locality), 모델의 편견 때문이 아니라 데이터의 통계적 특성(SNR)이 그렇게 하라고 시키기 때문입니다.
   • 결국 복잡한 딥러닝 모델도 뜯어보니 **"통계적으로 계산된 필터(Wiener Filter)"**와 똑같이 행동하고 있었습니다.

 

 

4 Validation

이 섹션에서는 우리의 주장을 뒷받침하기 위해 광범위한 검증을 수행합니다. Diffusion model의 main backbone으로, 우리는 [12]의 프로토콜을 따르기 위해 self-attention이 제거된 DDPM U-Net [8]을 사용합니다. 섹션 B.2에서 보여주듯이, self-attention을 제거하는 것은 성능에 큰 영향을 미치지 않으며, 우리의 통찰력은 두 architectures 모두에 유효합니다.

우리는 서로 다른 neural network architectures가 유사한 sensitivity fields를 학습하며, 이는 결과적으로 high-SNR principal components에 대한 projection operators, 즉 Wiener filter와 일치한다는 것을 보여주는 것으로 시작합니다. 우리는 학습된 sensitivity fields가 dataset의 속성임을 보여줌으로써 계속해서 data의 statistics를 조작하여 diffusion model의 sensitivity가 low noise levels에 대해 nonlocal이 되는 것을 포함하여 어떤 모양이든 취하도록 강제할 수 있음을 입증합니다.

마지막으로, trained diffusion models의 locality properties가 data statistics에서 비롯된다는 우리의 주장을 뒷받침하기 위해, 우리는 이전의 patch-based analytical models [12, 19]에 대한 간단한 수정을 제안합니다. Trained diffusion models로부터 locality를 측정하는 대신, 우리는 analytical model이 high-SNR principal components만 사용하도록 제한합니다. 우리는 이 수정을 5개의 datasets에서 벤치마킹하고, 이 알고리즘이 더 해석 가능하면서도 다른 baselines보다 trained diffusion models를 더 잘 설명한다는 것을 보여줍니다. 추가로, 우리는 우리 모델을 소거 분석(ablation)하고 섹션 B.1에서 비교를 제시합니다.

Locality pattern is shared across architectures. 우리는 CIFAR10 dataset에서 훈련된 architectures (U-Net [8] 및 diffusion transformer (DiT) [21]) 전반에 걸쳐 denoising process 동안의 locality patterns를 비교합니다. 비록 convolutional layers로 인해 U-Nets에는 locality에 대한 architectural bias가 있지만, DiTs의 self-attention layers는 모든 patch가 다른 모든 patch에 주의를 기울일 수 있는 global scope를 가집니다. 그럼에도 불구하고, Figure 2는 U-Nets와 DiTs가 유사한 sensitivity fields를 공유한다는 것을 보여줍니다. 놀랍게도, 이러한 fields는 high-SNR projector operators의 모양, 즉 Wiener filter의 sensitivity와 유사합니다. 이것은 diffusion models가 locality properties를 보이는 주된 이유가 dataset 내 images 간의 pixels의 correlation이라는 증거를 제공합니다. 우리의 관찰은 neural network architectural 선택이 data statistics를 정확하게 포착하는 데 중요하지만, diffusion models의 locality patterns의 주된 원인은 아니라는 것입니다.

Learned sensitivity fields are not always equivariant. 이전 실험에서 보았듯이, diffusion models에 의해 학습된 sensitivity fields는 architectures 전반에 걸쳐 유사하며 data의 principal components와 정렬됩니다. Figure 2에서, 이러한 fields는 대략적으로 isotropic하고 equivariant하게 보입니다—의미는 sensitivity $s^q(x)$가 각 pixel $q$에 대해 translation까지 동일한 모양을 갖는다는 것입니다. 이러한 형태의 sensitivity는 [12]의 square-shaped patches에 의해 잘 포착됩니다. 이러한 행동은 neighboring pixels 간의 높은 correlation과 다양한 natural images로 구성된 CIFAR10 dataset에 내재된 translation equivariance 때문에 발생합니다.

그러나 더 specialized datasets의 경우, principal components—그리고 결과적으로 학습된 sensitivity fields—는 급격히 다른 모양을 띠게 됩니다. 특히, CelebA-HQ는 균일하게 크기가 조정되고 중앙에 배치된 human faces의 dataset입니다. Translation equivariance의 부족과 독특한 pixel correlation patterns는 구조적이고 위치 의존적인(location-dependent) sensitivity fields를 초래합니다.

Figure 3에서, 우리는 CelebA-HQ에서 훈련된 diffusion model의 sensitivity fields에서 발생하는 복잡한 구조를 관찰합니다. 주목할 점은, sensitivity의 패턴이 이제 pixel의 위치에 크게 의존한다는 것입니다. 이 실험은 특히 specialized datasets의 경우, 이전 연구의 것보다 더 유연한 sensitivity fields 표현의 필요성을 강조합니다.

Manipulating the sensitivity field. 우리는 dataset의 statistics를 편집함으로써 neural denoisers의 sensitivity fields를 조작하고 어떤 모양이든 취하게 만들 수 있음을 보여줍니다. 이 조작을 통해, U-Net-based denoisers는 local하지 않은 sensitivity fields를 학습할 수 있으며, 따라서 학습된 denoisers의 locality properties가 dataset statistics로부터 나타난다는 것을 시사합니다.

CIFAR-10에 대한 실험에서, 우리는 수정된 dataset을 생성합니다:

$$\hat{x}_0 = x_0 + \gamma c s, \quad c \sim \text{Uniform}([-1, 1]^3),$$

여기서 $x_0 \in \mathbb{R}^d$는 training image이고, $s \in \{0, 1\}^d$는 문자 "W" 모양의 고정된 binary mask이며, $c \in \mathbb{R}^3$는 random RGB vector (image당 단일 색상)이고 $\gamma > 0$은 signal strength를 제어합니다. 이 변환은 $E[\gamma c s] = 0$이므로 data의 first-order moments를 변경하지 않는다는 점에 유의하십시오. 이를 통해, 우리는 수정된 CIFAR10 dataset에서 처음부터 새로운 DDPM U-Net을 훈련하고 그 sensitivity fields를 연구합니다. $\lambda_w$를 perturbation의 variance라고 합시다. 우리는 어떤 중간 $t^\star$에 대해 $\lambda_w \approx \sigma_{t^\star}$가 되도록 $\gamma$를 선택합니다. 즉, 추가된 signal의 variance가 noise의 variance와 일치하도록 합니다. Figure 4에서 볼 수 있듯이, $\sigma_t \ll \lambda_w$인 모든 $t$에 대해 "W" 모양의 sensitivity field가 나타납니다. 결정적으로, 이것은 data covariance에 패턴을 임베딩함으로써 훈련된 neural network의 sensitivity에서 원하는 어떤 패턴이든 유도될 수 있음을 입증합니다.

Our model. 이전 연구는 훈련된 denoisers의 sensitivity fields에 맞춰진 rectangular binary masks를 사용합니다. 본 논문에서, 우리는 훈련된 denoisers의 sensitivity fields가 data covariance로부터 나타난다는 것을 입증했습니다. 우리는 constant sensitivity fields를 고려합니다, 즉 $A^q_t$는 $x$의 함수가 아닙니다. Sensitivity field가 일정하다면 denoiser는 linear하며, 우리는 optimal linear denoiser가 Wiener filter라는 것을 알고 있습니다. 이 직관을 사용하여, 우리는 locality의 일반화된 개념을 고려하고 locality property가 subspace projection과 동일하다는 것을 보여줍니다. 이는 basis의 orthogonal change와 masking operator로 쓸 수 있습니다. 우리는 섹션 A.3에서 자세한 유도를 제공합니다.

[12, 19]에서처럼 측정된 sensitivity field를 high-SNR components에 대한 projection operator (optimal linear denoiser의 sensitivity)로 대체하는 것은 patch-based optimal denoisers와 동등하거나 더 나은 성능을 발휘합니다. 더 공식적으로, 우리는 다음 analytical model을 사용할 것을 제안합니다:

$$\hat{f}(x, t) = \sum_{i=1}^N w_i(x, t)x^{(i)}_0, \quad w^q_i(x) = \text{softmax}_i \left( -\frac{1}{2\sigma^2_t} \left\| \hat{W}^q_t \left( \frac{1}{\sqrt{\alpha_t}} x - x^{(j)}_0 \right) \right\|^2_2 \right)_{j \in [N]}, \quad (8)$$

여기서 $\hat{W}^q_t$는 threshold $\tau = 0.02$로 이진화된 Wiener matrix의 $q$-th row입니다 (달리 명시되지 않는 한 우리는 row의 max value에 대해 상대적으로 $\tau = 0.02$를 사용하고 있습니다). MNIST와 Fashion MNIST의 경우 우리는 $\tau = 0.005$를 사용합니다. 우리는 섹션 A.2와 B.1에서 이 공식의 자세한 유도와 $\tau$의 ablation을 제공합니다. [12] 및 [19]와 비교한 우리 모델의 주요 차이점은 다음과 같습니다:

1. Enhanced interpretability. Trained models에 patch sizes 및/또는 shapes를 맞추는 대신, 우리는 dataset statistics로부터 분석적으로 그것들을 얻습니다.
2. No equivariance. 이전 연구는 equivariance를 diffusion models의 중요한 속성으로 주장하지만 [12, 18], 우리는 대신 식 (8)에 translation group integral을 도입하는 것이 성능을 향상시키지 않고 inference time만 증가시킨다는 것을 발견했습니다.
3. Locality specific to each pixel in the image. 이전 연구와 달리, 우리는 patches의 모양이 image의 모든 pixels에 걸쳐 공유되도록 강제하지 않고, 대신 dataset의 statistics에 의존합니다. 이것은 faces의 datasets와 같이 nonlocal covariances를 가진 datasets에 특히 중요합니다.

우리의 모델은 nonlinear하며 dataset이 Gaussian이라고 가정하지 않습니다. 오히려, 이것은 dataset의 second-order statistics로 locality fields만을 근사합니다. 우리는 analytical model의 predictions와 동일한 starting noise가 주어진 trained DDPM [8] 사이의 $r^2$-coefficient of determination과 mean-squared error (MSE)를 측정하여 우리의 analytical model을 벤치마킹합니다.

비교를 위해, 우리는 다양한 통계 세트를 가진 5개의 datasets를 선택했습니다: 다양한 $32 \times 32$ natural images의 dataset인 CIFAR10 [16]; $64 \times 64$의 centered faces와 animals datasets인 CelebA-HQ [13]와 AFHQv2 [3]; 그리고 $28 \times 28$ 해상도의 binary centered images datasets인 MNIST [6]와 FashionMNIST [32]. 우리는 식 (3)의 vanilla optimal denoiser, Wiener filter [31], 그리고 Kamb와 Ganguli [12]의 patch-based optimal denoising algorithm과 비교합니다. 추가적으로, diffusion models의 signal-to-noise mapping의 variance를 포착하기 위해, 동일한 architecture와 dataset이지만 다른 weight initialization을 가진 또 다른 trained diffusion model과 비교합니다.

Table 1과 Figure 5는 우리의 analytical model이 모든 baselines보다 성능이 뛰어나며, Wiener filter가 거의 항상 2위를 차지한다는 것을 보여줍니다. Kamb와 Ganguli의 모델은 patch-based locality가 눈을 지우고 얼굴 특징을 흐리게 하기 때문에 CelebA-HQ에서 질적으로 더 나쁜 성능을 보이며, 반면 dataset-dependent locality를 사용하는 다른 모델들은 이러한 특징을 유지합니다. 이 실험은 analytical models에서 올바른 locality의 모델링이 trained diffusion models를 설명하는 데 핵심이며 그러한 localities가 dataset statistics로부터 온다는 우리의 가설을 확인합니다. 우리는 섹션 B.7에서 AFHQv2와 Fashion-MNIST에 대한 추가적인 정량적 결과를 제공합니다.

 

 

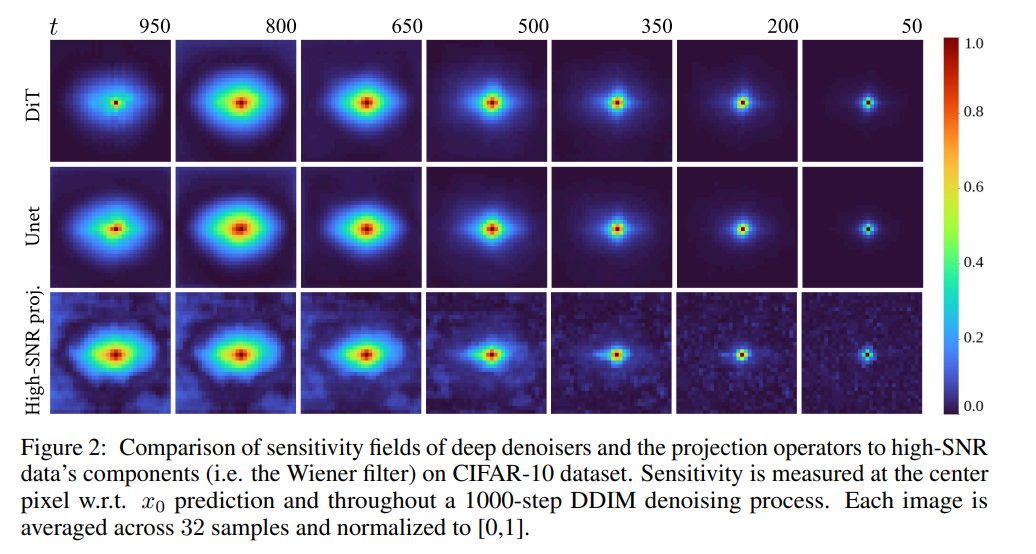
Figure 2: Architecture Agnostic Locality (구조와 상관없는 Locality)

이 그림은 **"모델의 구조(CNN vs Transformer)가 Locality를 결정하는 것이 아니다"**라는 주장을 시각적으로 증명합니다.

• 행(Rows) 설명:
  • DiT (Diffusion Transformer): Self-attention을 사용하여 이론적으로는 이미지 전체(Global)를 볼 수 있는 구조입니다.
  • Unet: Convolution을 사용하여 구조적으로 Locality(Inductive Bias)를 가지는 구조입니다.
  • High-SNR proj: 논문에서 제안한 데이터 통계 기반의 Wiener Filter (Optimal Linear Denoiser)입니다.
• 열(Columns) 설명: Noise level $t$가 950(High noise)에서 50(Low noise)으로 줄어드는 과정입니다.
• 핵심 분석:
  1. DiT $\approx$ U-Net: 구조가 완전히 다른데도 학습된 **Sensitivity Field(주황색/붉은색 영역)**가 놀랍도록 유사합니다. 즉, Transformer도 데이터 통계에 맞춰 스스로 Locality를 학습했다는 뜻입니다.
  2. Model $\approx$ Wiener Filter: 딥러닝 모델들의 Sensitivity가 통계적으로 계산된 High-SNR projection과 거의 일치합니다.
  3. Shrinkage: $t$가 줄어들수록(오른쪽으로 갈수록) Sensitivity 영역이 좁아지는데, 이는 노이즈가 줄어들수록 주변 픽셀보다 자기 자신(Identity)을 더 신뢰해야 한다는 이론과 일치합니다.

 

 

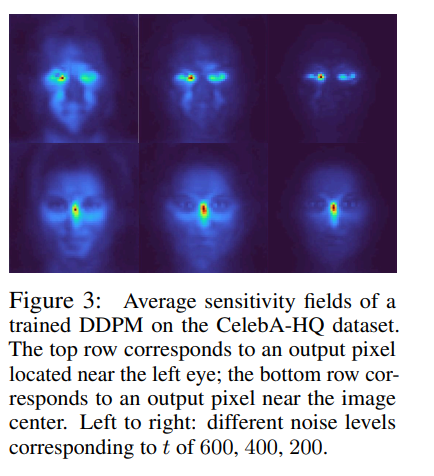
Figure 3: Non-local Correlations in CelebA-HQ (얼굴 데이터의 비국소적 상관관계)

이 그림은 **"Locality가 항상 단순한 원형/사각형(Isotropic)은 아니다"**라는 것을 보여줍니다. 기존 연구들이 간과한 부분입니다.

• 상황: CelebA-HQ(정렬된 얼굴 데이터셋)로 학습된 모델의 Sensitivity Field입니다.
• Top Row (왼쪽 눈 근처 픽셀):
  • 왼쪽 눈 픽셀을 복원할 때, 모델은 단순히 주변만 보는 게 아니라 반대쪽(오른쪽) 눈의 위치도 함께 참고합니다. (두 눈이 동시에 밝게 빛나는 것 확인 가능)
  • 이는 사람 얼굴의 대칭성(Symmetry)이라는 데이터 특성을 반영한 Non-local한 패턴입니다.
• Bottom Row (코/중앙 근처 픽셀):
  • 코 부분을 복원할 때는 얼굴 중앙부의 구조적 특징을 넓게 참고합니다.
• 핵심 분석:
  • 단순히 "좁은 사각형 패치"로 Locality를 정의했던 기존 연구(Kamb & Ganguli [12]) 방식은 이러한 복잡한 상관관계(Long-range dependency)를 끊어버리기 때문에 성능이 떨어질 수밖에 없습니다.

 

 

 

Figure 4: The "W" Manipulation Experiment (통계 조작 실험)

이 그림은 **"데이터 통계를 조작하면 모델의 시선(Sensitivity)도 조작된다"**는 것을 증명한 **결정적 증거(Smoking Gun)**입니다.

• 실험 설정:
  • CIFAR-10 데이터셋에 사람 눈에는 잘 안 띄는 미세한 **"W" 모양의 노이즈 패턴($\gamma c s$)**을 섞어서 학습시켰습니다.
  • Top Row: 원본 데이터로 학습. 일반적인 둥근 모양의 Sensitivity.
  • Middle Row (+0.1W): 약하게 "W" 패턴 추가. Sensitivity Field에 희미하게 "W" 형상이 나타남.
  • Bottom Row (+0.5W): 강하게 "W" 패턴 추가.
• 핵심 분석:
  • 하단(Bottom Row)을 보면, 노이즈가 줄어드는 특정 구간(빨간 밑줄)에서 모델의 Sensitivity Field가 선명한 "W" 모양을 띠고 있습니다.
  • 모델의 구조(U-Net)는 그대로인데 데이터의 공분산(Covariance)에 "W"를 심었더니 모델이 "W" 모양으로 쳐다보게 되었습니다.
  • 결론: "Locality는 모델의 Inductive Bias가 아니라, **Data Statistics(통계)**가 만들어내는 것이다."라는 논문의 주장을 완벽하게 입증합니다.

 

 

 

 

 

 

4 Validation 정리노트 (for AI Researcher)

1. Universality of Locality (Architecture Agnostic)

• Observation: CIFAR10에서 학습된 U-Net(CNN-based, Inductive bias $O$)과 DiT(Transformer-based, Global attention, Inductive bias $X$)의 Sensitivity fields를 비교.
• Result: 두 Architecture 모두 유사한 Sensitivity fields를 가지며, 이는 **High-SNR projector operators (Wiener filter)**의 형태와 일치함.
• Insight: Diffusion model의 Locality는 Neural network의 Architectural choice가 아니라, Dataset 내 Pixel 간의 Correlation (Data statistics)에서 기인함.

2. Data-Dependent Sensitivity Structure

• Natural Images (CIFAR10): Neighboring pixel 간의 Correlation이 높고 Translation equivariance가 존재 $\rightarrow$ Isotropic & Equivariant sensitivity (기존 연구 [12]의 가정과 일치).
• Specialized Datasets (CelebA-HQ): 정렬된 얼굴 데이터. Translation equivariance가 없고 Pixel 위치에 따른 상관관계가 다름 $\rightarrow$ Location-dependent & Non-local sensitivity.
• Limit of Prior Work: [12]의 Square-shaped patch 방식은 CelebA-HQ 같은 데이터에서 눈(Eye)과 같은 특징을 지우거나 흐리게 만듦.

3. Manipulation of Sensitivity (The "W" Experiment)

• Hypothesis Validation: Data statistics를 조작하면 Model의 Sensitivity도 조작 가능한가?
• Method: CIFAR10 이미지에 "W" 모양의 고정된 Binary mask 패턴($\gamma c s$)을 약하게 주입하여 학습.
• Result: 학습된 U-Net은 $\sigma_t \ll \lambda_w$ 구간에서 정확히 "W" 모양의 Sensitivity field를 학습함.
• Conclusion: Trained neural network의 Sensitivity pattern은 Data covariance에 임베딩된 패턴을 그대로 반영함.

4. Proposed Analytical Model (Generalized Locality)

• Concept: 기존 연구처럼 Trained model에서 Patch를 측정하는 대신, Dataset Statistics로부터 분석적으로 도출된 High-SNR principal components를 사용.
• Algorithm: Optimal Denoiser의 Weight 계산 시, Binarized Wiener Matrix ($\hat{W}^q_t$)를 마스크로 사용 (Eq. 8).
• $$w^q_i(x) = \text{softmax}_i \left( -\frac{1}{2\sigma^2_t} \left\| \hat{W}^q_t \left( \frac{1}{\sqrt{\alpha_t}} x - x^{(j)}_0 \right) \right\|^2_2 \right)$$
• Key Improvements:
  1. Interpretability: 학습된 모델 없이 통계적으로 도출 가능.
  2. No Equivariance Constraint: 강제적인 Translation group 적용은 성능 향상 없이 연산만 늘림 $\rightarrow$ 제거.
  3. Pixel-specific Locality: 모든 픽셀이 동일한 Patch를 공유하지 않고, 픽셀 위치마다 다른 통계적 Locality 적용 (Faces 데이터에 필수적).

5. Benchmark Results

• Setup: CIFAR10, CelebA-HQ, AFHQv2, MNIST, FashionMNIST.
• Performance: Proposed Model > Wiener Filter > Kamb & Ganguli [12] > Vanilla Optimal Denoiser.
• Finding: 단순한 Wiener filter가 기존의 복잡한 Patch-based method [12]보다 우수한 성능(2위)을 보임. 본 논문의 모델이 SOTA 달성.

---

쉬운 설명 :

"AI의 시선은 데이터가 결정한다 (증명 완료)"

1. 도구 탓 하지 마라:
2. 연구팀이 돋보기(CNN/U-Net)를 쓰든 망원경(Transformer/DiT)을 쓰든, AI가 그림을 그릴 때 집중하는 부위(Sensitivity)는 똑같았습니다. 심지어 그 모양은 수학적으로 계산한 '통계 필터(Wiener Filter)'와 똑같았습니다. 즉, AI가 좁게 보는 건 렌즈 때문이 아니라 데이터가 그렇게 생겨 먹어서였습니다.
3. 얼굴 데이터의 반란:
4. 풍경 사진(CIFAR10)은 어디를 봐도 비슷비슷해서 기존 연구처럼 "네모난 구멍으로 봐라"고 해도 잘 통했습니다. 하지만 사람 얼굴(CelebA-HQ)은 다릅니다. 눈은 항상 그 자리에 있고, 코는 코 자리에 있죠. 기존 방법대로 "네모난 구멍"을 강요했더니 AI가 눈코입을 뭉개버렸습니다. 본 논문의 모델은 **"데이터 통계상 눈은 눈끼리, 코는 코끼리 연결되어 있으니 모양을 자유롭게 바꿔!"**라고 허용해서 훨씬 선명한 결과를 얻었습니다.
5. "W"의 마법:
6. 연구팀은 자신들의 주장을 증명하기 위해 짓궂은 실험을 했습니다. 훈련 데이터에 사람 눈에는 안 보이는 아주 희미한 "W" 자 모양의 패턴을 숨겨놓았습니다. 그랬더니 AI 모델이 나중에 그림을 그릴 때 정확히 "W" 자 모양으로 데이터를 쳐다보는 것을 확인했습니다. AI가 데이터의 통계적 특징을 따라간다는 빼박 증거입니다.
7. 최종 결론:
8. "AI 모델 뜯어볼 필요 없다. 그냥 데이터 통계(Wiener Matrix)만 뽑아서 그걸로 필터를 만들면, 기존에 어렵게 만든 이론들보다 훨씬 더 잘 작동한다."

 

구조(Architecture)는 중요하지 않다"는 주장의 오류

장 큰 주장은 "Locality는 구조(Inductive Bias) 때문이 아니라, 데이터 통계 때문이다"라는 것인데. 하지만 이는 흑백논리에 가까움.

CNN(U-Net)은 태생적으로 Locality(지역성)를 강제하는 구조를 가지고 있음. 반면 Transformer(DiT)는 전역적(Global)이지만, 학습을 통해 데이터의 Locality를 "배우는" 것

만약 구조가 정말 상관없다면, MLP(Multi-Layer Perceptron) 처럼 공간 정보가 완전히 무시된 구조로도 동일한 성능과 Sensitivity Map이 나와야 함, 하지만 이는 불가능


"선형성(Linearity)"의 함정: 생성은 정말 선형적인가?
논문의 실험은 주로 Low Noise Regime(노이즈가 적은 구간, t->0)이나 Denoising 자체에 초점을 맞추고 있음. 이미지가 거의 다 만들어진 상태에서 노이즈를 살짝 걷어내는 건 당연히 선형 필터(Smoothing)와 비슷할 수밖에 없음

"W" 실험의 맹점 (상관관계 vs 인과관계)
데이터에 강제로 "W" 패턴을 심었으니 모델이 "W"를 배우는 건 당연한 결과(Tautology)
이것은 "데이터가 Sensitivity에 영향을 줄 수 있다"는 충분조건을 증명한 것이지, "구조적 편향(Inductive Bias)이 필요 없다"는 필요조건을 깬 것이 아님

 

만약 일반화가 "High-SNR(주로 저주파~중주파) 정보의 Pass-through" 때문에 일어나는 것이라면, 그 정보를 강제로 없앴을 때 모델이 어떻게 행동하는지를 보여줬어야 했음


"최신 모델이 위너 필터로 수렴한다"는 관찰은 훌륭하지만, "그렇게 되지 않도록 강제했을 때" 어떤 일이 벌어지는지 확인하지 않은 것은 과학적 검증의 큰 구멍

 

 

 

 

3.5점 / 5점

"Diffusion Model의 '선형적 복원 능력'을 해석하는 데는 성공했으나, '비선형적 창조 능력'을 설명하는 데는 실패한 절반의 성공."