LLM : 논문 리뷰 : Language Self-Play For Data-Free Training

용어 설명 (Glossary)

• Language Self-Play (LSP): 이 논문에서 제안하는 핵심 훈련 프레임워크. 하나의 LLM이 두 가지 역할(Challenger, Solver)을 수행하며 스스로 데이터를 생성하고 학습하는 과정.
• Challenger ( πCh ): Solver가 해결하기 어려운 어려운 질문(Instruction)을 생성하여 Solver의 Reward를 낮추려는 적대적(Adversarial) 역할을 하는 Agent 모드.​
• Solver ( πSol ): Challenger가 낸 질문에 대해 답변을 생성하고 Reward를 최대화하려는 Agent 모드.​
• LSP-Zero: Self-reward 정규화 없이 순수하게 Challenger와 Solver가 Zero-sum 게임을 하는 초기 형태.
• Self-Reward ( RQ ): 모델이 생성한 답변의 품질(Instruction following, clarity 등)을 모델 스스로 채점하여 보상으로 사용하는 기법. Adversarial process가 무의미한 텍스트 생성으로 변질되는 것을 막는 역할을 함.​
• Group-Relative Policy Optimization (GRPO): PPO와 유사하지만 Value function 모델 없이 그룹 내 샘플들의 상대적 우위를 통해 학습하는 RL 알고리즘. 이 논문의 베이스 최적화 기법.

---

Purpose of the Paper

• Data Bottleneck 극복: 기존의 LLM Post-training은 고품질의 instruction tuning dataset이나 human preference data에 전적으로 의존함. 이 논문은 외부 데이터 없이 모델의 성능을 향상시키는 Data-Free Training을 목표로 함.
• Dynamic Data Generation: 기존의 Synthetic data 방식은 고정된 데이터셋을 만들거나 더 큰 모델(Teacher)을 모방하는 데 그침. 이 연구는 훈련 데이터 자체를 **"학습하는 Agent (Challenger)"**로 정의하여, Solver의 실력이 늘어남에 따라 데이터(질문)의 난이도도 함께 진화하는 Perpetual improvement framework를 제안함.

---

Key Contributions & Novelty

• Game-Theoretic Framework (Adversarial Self-Play):
  • Contribution: 학습 과정을 Minimax Game으로 공식화함. Challenger는 Solver가 실패할(Reward가 낮을) 법한 질문을 생성하고, Solver는 그에 대한 답변을 생성하여 Reward를 최대화함.
  • Novelty: 별도의 Adversary 모델 없이 **단일 LLM ()**이 프롬프팅(Challenger prompt vs Solver role)만으로 두 역할을 수행하여 메모리 효율적이고 자율적인 학습이 가능함.
  • πθπθ
• Self-Refining Data Stream:
  • Contribution: 고정된 데이터셋을 반복 학습하는 것이 아니라, 훈련 과정 자체가 데이터 생성 과정이 되는 스트리밍 방식을 도입.
  • Novelty: 단순히 데이터를 많이 만드는 것이 아니라, Solver의 현재 약점을 파고드는 Targeted hard examples를 생성하도록 유도함.
• Stabilization via Self-Reward:
  • Contribution: 순수 Adversarial game이 "Python으로만 대답하기"와 같은 Reward Hacking이나 무의미한 난이도 상승으로 변질되는 것을 막기 위해, **Self-Reward ()**를 도입하여 Challenger와 Solver의 목적함수를 조정, High-quality interaction을 유지함.
  • RQRQ​

---

Experimental Highlights

• Experimental Setup:
  • Base Model: Llama-3.2-3B-Instruct
  • Baseline: Base Model, GRPO (Alpaca Data로 훈련된 지도학습 기반 RL)
  • Benchmark: AlpacaEval 2.0 (GPT-4o as a judge)
• Performance Results:
  • Data-Free vs Data-Driven: 외부 데이터(Alpaca Data)를 전혀 사용하지 않은 **LSP (40.6%)**가 데이터 기반 학습을 한 **GRPO (40.9%)**와 거의 동등한 성능을 달성함.
  • Conversational Task (Vicuna): 창의적이고 개방형 질문이 많은 Vicuna subset에서는 LSP가 Base model 및 GRPO보다 월등히 높은 승률을 기록함 (GRPO 28.7% vs LSP 46.3%). 이는 Challenger가 생성하는 다양한 상황극 프롬프트 덕분임.
• Continuous Improvement:
  • 이미 GRPO로 훈련된 모델(RL Model)을 초기값으로 사용하여 LSP를 적용한 결과, 승률이 40.9%에서 43.1%로 추가 상승함. 이는 LSP가 기존 RL 훈련 이후의 Next training stage로서 유효함을 증명.

---

Limitations and Future Work

• Limitations:
  • Reward Model Dependency: 실험이 선호도 기반(Preferential) Reward Model에 의존함. Reward Model의 편향이나 판단 능력의 한계가 곧 LSP 성능의 상한선이 됨.
  • Adversarial Degeneration: Self-reward 없이는 모델이 서로에게 무의미한 텍스트를 생성하거나 Reward를 해킹하는(예: 무조건 Python 코드 반환) Adversarial nonsense 패턴으로 빠지는 경향이 발견됨.
• Future Work:
  • Verifiable Rewards: 수학이나 코딩처럼 정답 검증이 명확한(Verifiable) 도메인에 적용하면 더 강력한 효과를 낼 것으로 기대.
  • Embodied AI: AI가 물리적 세계에서 스스로 경험(Data)을 수집하는 Embodied Agent로 확장될 때, 이 Self-play 프레임워크가 경험 수집의 주체성을 제공할 수 있음.
  • Query Diversity: 현재는 정형화된 패턴이 나타나기도 하므로, 더 다양한 스타일의 질문을 생성하도록 Challenger를 개선하는 연구 필요.

---

Overall Summary

이 논문은 외부 데이터 없이 LLM이 스스로 약점을 파악하는 질문을 생성(Challenger)하고 이를 해결(Solver)하는 경쟁적 게임(Self-Play)을 통해 성능을 향상시키는 Language Self-Play (LSP) 프레임워크를 제안합니다. Llama-3.2-3B 모델을 이용한 실험에서, LSP는 훈련 데이터가 전혀 없는 상황에서도 데이터 기반 RL 방법론(GRPO)과 대등한 성능을 보였으며, 특히 개방형 대화 테스크에서 뛰어난 성과를 입증했습니다. 이 연구는 데이터 고갈 문제(Data scarcity)에 직면한 LLM 분야에서, 모델이 스스로 고품질의 학습 데이터를 생성하고 진화할 수 있는 Autonomous Self-Improvement의 가능성을 열었다는 점에서 중요한 의의를 가집니다.

---

쉬운 설명 (Analogy)

이 논문의 아이디어는 **"혼자서 바둑을 두며 실력을 키우는 알파고"**를 언어 모델에 적용한 것과 같습니다.

• 기존 방식: 선생님(사람 혹은 더 똑똑한 AI)이 만들어준 문제집(Dataset)을 풀면서 공부합니다. 문제집이 떨어지면 더 이상 실력이 늘기 힘듭니다.
• 이 논문의 방식 (LSP):
  • 나의 분신 A(Challenger)는 "내가 가장 헷갈려할 만한 까다로운 문제"를 계속 출제합니다.
  • 나의 분신 B(Solver)는 그 문제를 풉니다.
  • 처음엔 쉬운 문제도 틀리지만, B가 문제를 잘 풀게 되면 A는 더 꼬아서 어려운 문제를 냅니다.
  • 이 과정에서 외부의 문제집 없이도 서로 경쟁하며 실력이 계속 늡니다.
  • 단, 문제가 너무 엉뚱해지지 않게 "좋은 문제와 답변의 기준"(Self-Reward)을 두어 품질을 관리합니다.

 

 

 

 

Abstract

Large language models (LLMs)는 최근 몇 년 동안 scale, 풍부한 고품질 training data, 그리고 reinforcement learning에 힘입어 빠르게 발전했습니다. 그러나 이러한 발전은 근본적인 bottleneck에 직면해 있는데, 바로 models가 지속적으로 학습하기 위해 끊임없이 더 많은 data가 필요하다는 점입니다.

본 연구에서는 additional data 없이 models가 개선될 수 있도록 하여 이러한 의존성을 제거하는 reinforcement learning approach를 제안합니다. 우리의 method는 self-play라는 game-theoretic framework를 활용합니다. 여기서 model의 capabilities는 competitive game에서의 performance로 간주되며, model이 자기 자신과 대결하게 함으로써 더 강력한 policies가 등장하게 됩니다. 우리는 이 과정을 Language Self-Play (LSP)라고 부릅니다.

Instruction-following benchmarks에서 Llama-3.2-3B-Instruct를 사용한 experiments는 pretrained models가 self-play만으로도 challenging tasks에서의 performance를 향상시킬 수 있을 뿐만 아니라, data-driven baselines보다 더 효과적으로 수행할 수 있음을 보여줍니다.

 

 

 

 

1 Introduction

Massive datasets에서 trained된 Large language models (LLMs)는 수많은 instruction following 및 reasoning tasks를 인간 전문가 수준으로 마스터하기 시작했습니다. Pre-training이라고 알려진 training의 초기 단계에서 trained model은 방대한 양의 정보를 흡수하지만, reinforcement learning (RL)과 같은 post-training 기술은 model이 바람직한 행동을 개발하고 specialized tasks에서 전문성을 갖추도록 합니다.

RL paradigm은 대중적인 predictive 또는 generative learning paradigms와 매우 다릅니다. 이들이 label을 predict하거나 data 자체를 reconstruct하려고 시도하는 반면, RL은 model에 명확한 target을 설정하지 않습니다. 대신, 제시된 시나리오에 반응하여 actions를 취함으로써 model은 reward라고 알려진 feedback을 보내는 environment에서 작동합니다. RL algorithms는 reward를 최대화하도록 agent의 행동을 구성합니다. 따라서 human preference-based rewards는 LLMs를 인간의 선호도 및 가치와 aligning할 수 있게 하며, task rewards는 LLMs가 specific tasks에서 개선되도록 돕습니다.

그럼에도 불구하고, super-human 범위의 기술을 얻을 잠재력을 제공함에도, RL은 모든 machine learning paradigms의 약점인 data에 대한 의존성을 공유합니다. 예측해야 할 구체적인 targets가 필요 없기는 하지만, RL methods는 LLM context에서 prompts의 형태를 취하는 task examples의 가용성에 의존하며, 따라서 동일한 bottleneck에 직면합니다. 이 문제를 우회하기 위해, LLM community는 synthetic data를 통한 training과 meta-learning 수단을 통해 가용한 data를 더 효율적으로 활용하는 방향으로 관심을 돌렸습니다. 본 논문에서 우리는 다른 approach를 취하며, data의 streaming을 RL agent가 취하는 actions로 공식화함으로써 data로부터의 training을 완전히 배제하는 training 기술을 소개합니다.

본 연구는 연속적인 iterations가 LLM과 그것이 학습하는 examples의 distribution을 모두 개선하는 algorithm을 소개합니다. 이를 위해, 우리는 players 중 하나는 점점 더 challenging한 queries를 generate하는 법을 배우고, 다른 하나는 이에 응답하는 법을 배우는 competitive game을 정의합니다. Self-play를 활용함으로써, 이 algorithm은 adversarial expert 없이 오직 하나의 LLM만을 사용하여 이 과정을 유도하며, 따라서 이 training을 autonomous하게 만듭니다.

우리는 AlpacaEval의 instruction-following tasks에서 Llama-3.2-3B-Instruct에 적용된 Language Self-Play (LSP)라고 명명된 이 기술로 실험했습니다. 우리의 실험 결과는 이러한 training이 풍부한 training data에 의존하는 LLMs의 performance만큼 강력하거나 더 강력한 performance를 가진 models를 제공한다는 것을 보여줍니다.

 

 

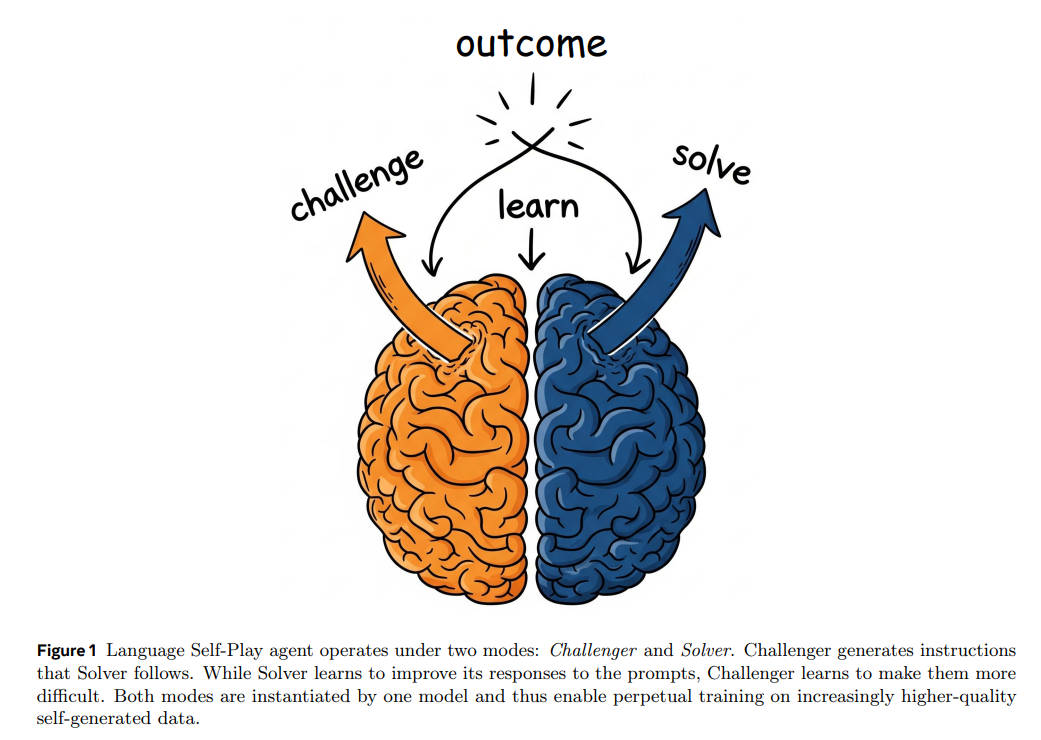
Figure 1: Language Self-Play agent는 두 가지 modes, 즉 Challenger와 Solver 하에서 작동합니다. Challenger는 Solver가 수행할 instructions를 generate합니다. Solver가 prompts에 대한 responses를 개선하는 법을 배우는 동안, Challenger는 그 문제들을 더 어렵게 만드는 법을 배웁니다. 두 modes는 하나의 model에 의해 구현되므로 점점 더 높은 품질의 self-generated data에 대한 끊임없는 training을 가능하게 합니다

 

 

1 Introduction 핵심 정리 (Researcher Note)

1. Problem Definition: RL의 Data Dependency

• Post-training 단계의 **Reinforcement Learning (RL)**은 predictive/generative learning과 달리 명확한 target 없이 reward를 최대화하는 방향으로 학습함.
• 하지만 RL 역시 prompts 형태의 task examples(Data)가 필요하다는 점에서 여전히 data bottleneck 문제에 직면함.
• 기존의 Synthetic data나 meta-learning 접근법과 달리, 본 연구는 외부 데이터 의존성을 완전히 제거하는 새로운 접근법을 제시함.

2. Proposed Method: Language Self-Play (LSP)

• Core Concept: Data streaming 과정을 RL agent의 actions로 공식화하여, training data 없이 학습하는 기법.
• Mechanism:
  • Competitive game 프레임워크 도입: 한 쪽은 점점 더 어려운 queries를 생성하고, 다른 한 쪽은 이에 응답하는 대결 구도.
  • Self-play 활용: Adversarial expert 없이 단일 LLM이 스스로 대결하며 autonomous하게 학습.
• Effect: LLM의 성능 향상과 학습에 사용되는 examples의 distribution 개선이 동시에 이루어짐 (Iterative improvement).

3. Experiments & Results

• Model: Llama-3.2-3B-Instruct
• Task: Instruction-following tasks (AlpacaEval)
• Key Finding: LSP로 학습된 모델이 방대한 training data에 의존하는 baselines와 동등하거나 더 강력한 performance를 달성함.

---

쉬운 설명 :

이 논문의 Introduction은 LLM을 더 똑똑하게 만드는 방법에 대한 이야기입니다. 보통 AI를 더 공부시키려면(RL), 사람이 만든 수많은 문제집(Data, Prompts)이 필요합니다. 그런데 이 "문제집"을 구하는 게 점점 어렵고 한계가 있습니다.

그래서 연구진은 **Language Self-Play (LSP)**라는 방법을 제안합니다. 쉽게 말해, AI가 스스로 문제를 내고 스스로 그 문제를 푸는 방식입니다.

• 외부에서 데이터를 가져오는 게 아니라, AI 안에서 "문제를 어렵게 내는 나"와 "그걸 맞추려는 나"가 서로 경쟁(Game)하게 만듭니다.
• 이 과정을 반복하면 외부의 도움 없이도 AI가 스스로 고난이도 문제를 만들어내고 해결하면서 점점 똑똑해집니다.

실제로 이 방법을 써보니, 데이터를 잔뜩 넣어 공부시킨 모델보다 혼자서 수련한 모델(LSP)이 더 일을 잘하거나 비슷하더라는 것이 핵심 내용입니다.

 

 

 

2 Language Self-Play

이 section에서, 우리는 LLM training을 bottleneck하는 training data 의존성 문제에 대한 우리의 solution을 제안합니다. 우리의 approach는 다음 관찰에서 비롯됩니다: dataset 자체가 learning agent라면, learning model이 발전함에 따라 새롭고 점점 더 challenging data를 제공하는 것이 가능해질 것입니다.

따라서, trained LLM 외에도, 점점 더 challenging instructions를 streaming하는 것을 다른 LLM의 actions로 model 할 수 있습니다. 명확성을 위해, 우리는 그 model을 Challenger라고 부르고 $\pi_{\text{Ch}}$로 표기하며, instructions를 따르는 model은 Solver라고 부르고 $\pi_{\text{Sol}}$로 표기합니다. 이 agents 간의 interaction은 Challenger에 의한 query generation step, $q \sim \pi_{\text{Ch}}(q)$와 Solver에 의한 query-answering step, $a \sim \pi_{\text{Sol}}(a|q)$로 구성됩니다. Solver는 task reward $R(q, a)$를 maximize하려고 시도하고, 이는 verification-based이거나 preference-based일 수 있으므로, Challenger는 reward를 minimize하는 것을 목표로 하여 점점 더 challenging queries를 generate하도록 자신의 behavior를 guide할 수 있습니다. 따라서, agents는 다음의 minimax game을 play하게 됩니다.

$$\min_{\pi_{\text{Ch}}} \max_{\pi_{\text{Sol}}} \mathbb{E}_{q \sim \pi_{\text{Ch}}, a \sim \pi_{\text{Sol}}} [R(q, a)]. \quad (1)$$

앞서 논의했듯이, 이 game을 통해 playing하고 learning하는 것은 training data가 없는 상황에서도 Solver가 improve할 수 있게 해줍니다. 그러나 얼핏 보면, $\pi_{\text{Ch}}$를 representing하는 데 additional model이 필요하다고 생각할 수 있습니다. 이는 우리를 adversarial training에 놓이게 하는데, 이는 adversary를 위한 extra memory를 필요로 할 뿐만 아니라 악명 높게 unstable합니다. 다행히도, competing players가 action space를 공유하는 competitive games는 self-play에 의해 효과적으로 해결됩니다. 두 players 모두 language models이므로, 그들은 tokens의 space에서 operate하며, 이는 우리가 self-play 설정을 채택하고 single model $\pi_\theta$를 사용하여 두 players를 instantiate할 수 있게 해줍니다. 따라서, 우리는 special challenger prompt (Box 1 참조)로 model을 prompting하여 Challenger를 represent합니다. 이와 같이, 우리는 Challenger를 $\pi_{\text{Ch}}^\theta(q) = \pi^\theta(q|< \text{cp} >)$로, Solver를 $\pi_{\text{Sol}}^\theta(a|q) = \pi^\theta(a|q)$로 modeled하여 game을 play합니다.

Challenger에 의해 generate된 prompts의 examples는 Box 2를, Solver의 responses는 Box 4 (Appendix A)를 참조하십시오.

Game을 efficient RL process로 전환하기 위해, 우리는 GRPO의 group-relative trick을 invoke하는 것이 자연스럽다는 것을 발견했습니다. 구체적으로, 각 iteration에서 우리는 Challenger가 $N$개의 queries $q_1, \dots, q_N$을 generate하게 합니다.

그런 다음, 각 query $q_i$에 대해, Solver는 $G$개의 answers $a^1_i, \dots, a^G_i$를 generate하고, 이들은 각각 rewards $R(q_i, a^1_i), \dots, R(q_i, a^G_i)$를 받습니다. 그런 다음, group value를 다음과 같이 calculating하면

$$V(q_i) = \frac{1}{G} \sum_{j=1}^G R(q_i, a^j_i) \quad (2)$$

query $q_i$에 대한 각 response의 relative advantage인 $A_{\text{Sol}}(q_i, a^j_i) = R(q_i, a^j_i) - V(q_i)$를 compute하기 위한 baseline을 얻을 수 있을 뿐만 아니라, Challenger가 maximize하고자 하는 query difficulty의 개념을 도출할 수 있습니다. 구체적으로, Challenger에게 $-V(q_i)$로 rewarding함으로써, 우리는 Solver의 performance가 부족한 영역을 probe하는 queries를 generate하도록 장려합니다. 따라서, 이 reward를 기반으로 하고 baseline $V = \frac{1}{N} \sum_{i=1}^N V(q_i)$를 정의하여, 우리는 Challenger의 advantage function을 다음과 같이 derive하고

$$A_{\text{Ch}}(q_i) = V - V(q_i) \quad (3)$$

KL-divergence regularization과 함께 이 advantage values로 두 players 모두에 대해 RL update를 수행합니다. 따라서, interactions의 sample $\{q_i, \{a^j_i\}_{j=1}^G\}_{i=1}^N$에 대해, Solver와 Challenger를 위한 loss functions는 각각 다음과 같습니다.

$$\text{Solver } L_{\text{Sol}}(\theta) = -\frac{1}{NG} \sum_{i=1}^N \sum_{j=1}^G \left[ \frac{\pi_{\text{Sol}}^\theta(a^j_i|q_i)}{\bot\pi_{\text{Sol}}^\theta(a^j_i|q_i)} A_{\text{Sol}}(q_i, a^j_i) - \beta \log \frac{\pi_{\text{Sol}}^\theta(a^j_i|q_i)}{\pi_{\text{Ref}}(a^j_i|q_i)} \right] \quad (4)$$

$$\text{Challenger } L_{\text{Ch}}(\theta) = -\frac{1}{N} \sum_{i=1}^N \left[ \frac{\pi_{\text{Ch}}^\theta(q_i)}{\bot\pi_{\text{Ch}}^\theta(q_i)} A_{\text{Ch}}(q_i) - \beta \log \frac{\pi_{\text{Ch}}^\theta(q_i)}{\pi_{\text{Ref}}(q_i)} \right] \quad (5)$$

여기서 $\bot$는 stop-gradient/detach operation을 나타냅니다. 이 losses는 함께 더해지고 $\theta$에 대해 differentiated되며, 그 후 gradient step이 취해집니다. 여기서 KL-divergence regularization이 중추적인 역할을 한다는 점은 주목할 가치가 있습니다. 전통적으로는 fine-tuned model이 reference model $\pi_{\text{Ref}}$에서 단순히 너무 많이 deviate하지 않도록 보장하지만, 여기서는 또한 Challenger가 semantic meaning이 없는 adversarial sequences를 무분별하게 generate하는 것을 방지합니다. 우리는 이 approach를 Language Self-Play Zero (LSP-Zero)라고 부르며, 여기서 Zero는 zero-sum을 의미하고, Section 4에서 AlpacaEval benchmark에 대해 이를 evaluate합니다.

위의 self-play 설정은 LLM의 영구적인 self-improvement를 초래하는 indefinite training을 자연스럽게 유도하는 것처럼 보일 수 있습니다. 그러나 우리의 일부 experiments에서, 우리는 결국 play가 adversarial nonsense로 degenerate된다는 것을 발견했습니다. 예를 들어, OpenAssistant의 reward-model-deberta-v3-large-v2로 작업하는 동안 관찰된 일반적인 pattern은 Solver가 대부분의 queries에 대해 Python으로 responding함으로써 수행하는 reward-hacking이었으며, 이는 명백히 도움이 되지 않았습니다. 따라서, play를 high-quality interaction으로 guide하기 위해, 우리는 reference model을 적절히 prompting하여 generate하는 quality self-reward $R_Q(q_i, a^j_i)$를 추가하는 것이 매우 도움이 된다는 것을 발견했습니다. 정확한 prompt2는 Box 3를 참조하십시오. 우리는 advantage 및 loss functions를 computing하기 전에 quality score를 Solver의 reward, $R(q_i, a^j_i) + R_Q(q_i, a^j_i)$에 추가하고, 또한 그 average인 $V_Q(q_i) = \frac{1}{G} \sum_{j=1}^G R_Q(q_i, a^j_i)$를 Challenger의 reward, $-V(q_i) + V_Q(q_i)$에 추가합니다. 일단 calculated되면, self-reward는 두 players의 rewards에 모두 추가되어, game은 더 이상 zero-sum이 아니게 됩니다. 이것이 적용되면, 우리는 self-play training이 효과적으로, 무기한으로 수행될 수 있음을 발견했습니다.

우리는 Language Self-Play (LSP)라고 부르는 전체 algorithm을 Algorithm 1의 pseudocode로 summarize합니다.

 

2 Language Self-Play 핵심 정리 (Researcher Note)

1. Conceptual Framework: Minimax Game

• Core Idea: Training data의 dependency를 제거하기 위해 Dataset 자체를 Learning agent로 대체.
• Game Definition: Challenger ($\pi_{\text{Ch}}$)와 Solver ($\pi_{\text{Sol}}$) 간의 Minimax game.
  • Challenger: Solver의 reward를 minimize하는 방향(즉, 어려운 문제 출제)으로 Query $q$를 generate.
  • Solver: Task reward $R(q, a)$를 maximize하는 방향으로 Answer $a$를 generate.
  • Objective: $\min_{\pi_{\text{Ch}}} \max_{\pi_{\text{Sol}}} \mathbb{E}[R(q, a)]$

2. Implementation: Single Model Architecture

• Efficient Self-Play: 별도의 Adversarial model을 두지 않고, 단일 Model $\pi_\theta$가 Prompt (e.g., special challenger prompt)에 따라 두 역할을 모두 수행.
  • $\pi_{\text{Ch}}^\theta(q) = \pi^\theta(q|< \text{cp} >)$
  • $\pi_{\text{Sol}}^\theta(a|q) = \pi^\theta(a|q)$
• Token Space Sharing: 두 player가 동일한 token space를 공유하므로 Adversarial training의 instability와 memory cost 문제를 완화.

3. Optimization: GRPO-based Advantage

• Group Relative Policy Optimization (GRPO) 방식을 채택하여 Group value $V(q_i)$를 baseline으로 활용.
• Reward Structure:
  • Solver Advantage: $A_{\text{Sol}}(q_i, a^j_i) = R(q_i, a^j_i) - V(q_i)$ (평균보다 잘했는가?)
  • Challenger Advantage: $A_{\text{Ch}}(q_i) = V - V(q_i)$ (전체 평균 $V$보다 해당 쿼리의 평균 점수 $V(q_i)$가 낮은가? 즉, Solver가 어려워했는가?)
• Loss Function: 일반적인 RL loss에 KL-divergence regularization을 추가.
  • KL의 역할: Challenger가 의미 없는(semantic meaning이 결여된) Adversarial sequence를 생성하는 것을 방지하는 핵심 역할.

4. Stability Strategy: From Zero-Sum to Non-Zero-Sum (LSP)

• Problem (LSP-Zero): 순수 Zero-sum 게임에서는 Solver가 Reward-hacking을 하거나(예: 무조건 Python 코드 출력), Challenger가 Adversarial nonsense를 생성하여 게임이 붕괴됨.
• Solution (Quality Self-Reward): Reference model을 이용해 Quality self-reward $R_Q$를 생성하여 두 Player 모두에게 부여.
  • Modified Challenger Reward: $-V(q_i) + V_Q(q_i)$
  • Effect: 게임이 Non-zero-sum으로 변환되며, 난이도는 높이되(Hard) 품질은 유지(High-quality)하는 방향으로 Indefinite training이 가능해짐.

---

쉬운 설명 :

이 섹션은 **"어떻게 AI 혼자서 무한히 똑똑해질 수 있는가?"**에 대한 구체적인 방법을 설명합니다.

• 1인 2역 (지킬 앤 하이드): AI 모델 하나가 두 가지 역할을 맡습니다.
  • Challenger (선생님): 학생이 틀릴 법한 아주 어려운 문제를 냅니다.
  • Solver (학생): 선생님이 낸 문제를 최선을 다해 풉니다.
• 점수 계산법 (Zero-sum):
  • 학생이 100점을 맞으면 선생님은 0점을 받습니다. (문제가 너무 쉬웠다는 뜻)
  • 학생이 0점을 맞으면 선생님은 100점을 받습니다. (문제를 아주 어렵게 잘 냈다는 뜻)
  • 이러면 선생님은 점수를 따기 위해 점점 더 어려운 문제를 개발하고, 학생은 살기 위해 점점 더 공부를 열심히 하게 됩니다.
• 문제점과 해결책 (LSP의 핵심):
  • 그냥 놔두면 선생님이 학생을 골탕 먹이려고 "아르르르 까꿍 @#$%" 같은 말도 안 되는 문제(Nonsense)를 내기 시작합니다. 학생이 못 맞추면 선생님 이득이니까요.
  • 그래서 연구진은 **"품질 점수(Quality Reward)"**라는 규칙을 추가했습니다. 문제가 말이 되고 수준이 높아야만 선생님도 점수를 받을 수 있게 바꾼 것입니다.
  • 이제 선생님은 **"말이 되면서도 학생이 풀기 어려운 문제"**를 내야 하고, 덕분에 AI는 이상한 길로 빠지지 않고 계속해서 고품질의 학습을 할 수 있게 됩니다.

 

 

 

 

 

주인장 이해

 N개의 질문을 만들어서 G개의 답변을 통해 업데이트

 

 

기존 GRPO는 G개의 답변으로만 업데이트를 했다면 N개의 질문이 배치가 되는 셈

왜? 질문마다 평균점수를 계산해야하기 때문