시계열 : 논문리뷰 : BasisFormer: Attention-based Time Series Forecasting with Learnable and Interpretable Basis

Abstract

 

기저(bases)는 feature extractor 또는 미래 참조 역할을 수행하는 능력 덕분에 최신 딥 러닝 기반 시계열 예측 모델의 필수적인 부분이 되었습니다. 효과적인 기저는 특정 시계열 데이터 세트에 맞춰져야 하고 세트 내의 각 시계열과 뚜렷한 상관관계를 나타내야 합니다. 그러나 현재 최첨단 방법들은 이러한 두 가지 요구 사항을 동시에 충족하는 능력이 제한적입니다. 이러한 문제를 해결하기 위해, 본 논문에서는 학습 가능하고 해석 가능한 기저를 활용하는 end-to-end 시계열 예측 architecture인 BasisFormer를 제안합니다.

이 architecture는 세 가지 구성 요소로 이루어져 있습니다. 첫째, 시계열의 과거 및 미래 부분을 두 개의 별개의 view로 취급하고 contrastive learning을 사용하는 적응형 self-supervised learning을 통해 기저를 획득합니다. 다음으로, bidirectional cross-attention을 통해 과거 view에서 시계열과 기저 간의 유사도 계수를 계산하는 Coef 모듈을 설계합니다. 마지막으로, 유사도 계수를 기반으로 미래 view에서 기저를 선택하고 통합하여 정확한 미래 예측을 생성하는 Forecast 모듈을 제시합니다. 6개의 데이터 세트에 대한 광범위한 실험을 통해 BasisFormer가 univariate 및 multivariate 예측 작업에서 이전의 최첨단 방법보다 각각 11.04% 및 15.78% 뛰어난 성능을 보임을 입증했습니다.

 

 

주요 아이디어:

• 시계열 예측에서 기저(bases)는 중요한 역할을 하지만, 기존 방법들은 데이터 특성에 맞는 기저를 찾고 각 시계열과의 상관관계를 파악하는 데 어려움이 있었음.
• BasisFormer는 이러한 문제를 해결하기 위해 학습 가능하고 해석 가능한 기저를 사용하는 새로운 end-to-end 시계열 예측 architecture임.

핵심 구성 요소:

1. 적응형 자기 지도 학습 (Adaptive Self-Supervised Learning):
   • 시계열 데이터의 과거와 미래 부분을 두 개의 다른 view로 보고, contrastive learning을 통해 데이터 자체에서 기저를 학습.
   • 즉, 데이터에 최적화된 기저를 자동으로 찾아냄.
2. Coef 모듈:
   • Bidirectional cross-attention 메커니즘을 사용하여 과거 시계열 데이터와 학습된 기저 사이의 유사도 계수를 계산.
   • 각 시계열에 어떤 기저가 중요한지 파악.
3. Forecast 모듈:
   • 계산된 유사도 계수를 기반으로 미래 시계열 예측에 필요한 기저를 선택하고 결합.
   • 최적의 기저 조합을 통해 정확한 예측을 생성.

성능:

• 6개의 데이터 세트에서 실험한 결과, BasisFormer는 기존 최첨단 방법보다 univariate 예측에서 11.04%, multivariate 예측에서 15.78% 더 뛰어난 성능을 보임.

장점:

• 데이터 적응성: 자기 지도 학습을 통해 특정 시계열 데이터에 맞는 기저를 학습하여 예측 성능을 향상시킴.
• 해석 가능성: 학습된 기저는 해석 가능하므로 예측 결과를 이해하고 분석하는 데 도움이 됨.
• End-to-End 학습: 전체 architecture가 end-to-end로 학습되어 최적화가 용이함.

참고:

• Contrastive Learning: 서로 다른 두 view의 데이터에서 유사한 특징은 가깝게, 다른 특징은 멀게 학습하는 방법.
• Bidirectional Cross-Attention: 두 개의 시퀀스 데이터에서 서로의 정보를 참조하여 관계를 파악하는 attention 메커니즘.

 

 

 

1 Introduction

 

추세 및 계절성과 같은 기저(bases)는 시간에 따른 데이터 변화의 핵심 요인으로 작용하고 기본적인 시간 패턴을 포착하기 때문에 시계열 모델링 및 예측에 필수적입니다. 예를 들어, 계절성은 제품 또는 서비스에 대한 수요의 규칙적인 변동을 포착할 수 있는 반면, 추세는 시장 또는 산업의 장기적인 성장 또는 감소를 반영할 수 있습니다. 이러한 기저를 시계열 모델에 통합하면 미래 행동에 대한 이해와 예측을 향상시킬 수 있습니다. 실제로 시계열 예측에 일반적으로 사용되는 모든 딥 러닝 모델은 기저 기반 모델로 재해석될 수 있습니다. N-BEATS, N-HiTS 및 FiLM은 모두 Fourier 및 Legendre 기저와 같은 명시적 기저를 사용합니다. 더 일반적으로, MLP (또는 CNN)의 선형 (또는 컨볼루션) 레이어는 시계열을 분해하는 필터 뱅크 역할을 하므로 암시적 기저로 간주될 수 있습니다. 또한 RNN 및 Transformers의 공변량 임베딩 (일명 전역 타임스탬프 임베딩)은 미래 시퀀스 예측을 위한 참조 지점을 제공하기 때문에 또 다른 형태의 기저입니다.

시계열 예측에 기저를 적용하려면 세 단계가 필요합니다.

 

우선, 해당 시계열 세트에 적합한 기저를 선택하거나 학습해야 합니다. 실제로 기저의 전체 공간은 매우 클 수 있는 반면, 세트 내 시계열의 패턴은 종종 유사합니다. 따라서 시계열 데이터의 특정 특성 (예: 주기 또는 빈도)에 맞는 기저를 학습하는 것이 바람직합니다. 이는 예측 모델의 복잡성을 줄이고 더 정확하고 해석 가능하게 만드는 데 도움이 될 수 있습니다.

 

둘째, 세트의 각 시계열은 기저에 따라 분해됩니다. 여기에는 기저의 각 벡터 (즉, 필터)에 대한 시계열의 유사성 또는 투영 에너지를 결정하는 계수 또는 가중치를 계산하는 작업이 포함됩니다. 각 시계열은 고유한 패턴과 특성을 나타내므로 이러한 계수는 시계열마다 다릅니다. 예를 들어, 서로 다른 시계열에 해당하는 Fourier 계수는 서로 다릅니다.

 

마지막으로, 예측은 기저의 미래 부분의 가중치 집계에 의해 결정됩니다.

 

불행히도 앞서 언급한 최첨단 방법들은 처음 두 단계의 요구 사항을 동시에 충족하는 데 어려움을 겪습니다. 한편으로, N-BEATS, N-HiTS 및 FiLM과 같이 고전적인 기저에 의존하는 방법들은 종종 기저가 학습 가능하지 않다고 가정하고, 기저에 투영할 때 각 시계열의 계수를 유연하게 학습합니다. 그러나 주어진 기저가 시계열 세트에 해당하는 모든 주기 또는 빈도를 포함한다는 보장이 없기 때문에 이러한 기저는 시간 패턴을 효과적으로 설명하지 못할 수 있습니다. 반면에 MLP, CNN, RNN, Transformer 및 그 변형과 같이 데이터에서 기저를 적응적으로 학습하는 것을 목표로 하는 방법들은 종종 기저와 개별 시계열 간의 유연한 연결의 필요성을 간과합니다. 특히, Transformer 및 그 변형은 공변량 임베딩을 학습하지만, 제한된 방식으로 동일한 임베딩을 다른 시계열 임베딩에 추가하거나 연결합니다. MLP 및 CNN의 경우 모든 시계열에 대해 동일한 선형 및 컨볼루션 레이어를 채택합니다.

 

앞서 언급한 난제를 효과적으로 해결하려면 데이터 세트의 고유한 특성을 정확하게 반영할 수 있는 기저를 얻고 예측 목적으로 기저에서 관련 벡터를 선택적으로 활용할 수 있는 예측 네트워크를 고안하는 것이 필수적입니다. 이 목표를 향해 나아가기 위해, 본 논문에서는 학습 가능하고 해석 가능한 기저를 갖춘 시계열 예측 architecture인 BasisFormer를 제안합니다. 첫 번째 단계로, 데이터에서 적응형 자기 지도 학습을 통해 기저를 획득합니다. 여기에는 시계열의 과거 및 미래 섹션을 두 개의 별개의 view로 취급하고, 시계열에 대한 기저 선택이 두 view에서 일관되어야 한다는 가정 하에 contrastive learning을 사용하여 기저를 학습하는 것이 포함됩니다. 그런 다음, 양방향 교차 attention을 통해 과거 view에서 시계열과 기저 간의 유사성을 측정하는 Coef 모듈을 설계하여 개별 시계열과 기저 간의 유연한 연결을 용이하게 합니다. 마지막으로, Coef 모듈에서 생성된 유사성에 따라 미래 view에서 기저의 벡터를 통합하여 정확한 미래 예측을 생성하는 Forecast 모듈을 개발합니다. 위의 세 부분은 end-to-end 방식으로 학습됩니다. 요약하면, 본 연구의 주요 기여는 다음과 같습니다.

• 시계열의 과거 및 미래 섹션을 두 개의 별개의 view로 취급하고 contrastive learning을 사용하여 기저 학습을 위한 자기 지도 방법을 제안합니다. 이는 시계열에 대한 기저 선택이 두 view에서 일관성을 유지하도록 합니다.
• 과거 view에서 시계열과 기저 간의 유사성을 측정하는 계수를 기반으로 미래 view에서 관련 기저를 선택하고 병합하는 Coef 및 Forecast 모듈을 설계합니다.
• 6개의 데이터 세트에 대한 광범위한 실험을 수행했으며, 본 모델이 이전의 SOTA 방법보다 univariate 예측 작업에서 11.04%, multivariate 예측 작업에서 15.78% 뛰어난 성능을 보임을 발견했습니다.

 

 

 

 

주요 내용:

• 시계열 예측에서 기저(bases)의 중요성을 강조하고, 기존 딥러닝 모델들이 기저를 활용하는 방식을 설명합니다.
• 기존 방법들의 한계점을 지적하고, BasisFormer가 이를 해결하기 위한 새로운 방법임을 제시합니다.

기저 (Bases) 란?

• 시계열 데이터의 근본적인 패턴 (추세, 계절성 등)을 포착하는 요소.
• 예측 모델의 정확도와 해석 가능성을 높이는 데 중요한 역할을 함.

기존 방법의 문제점:

• 고정된 기저: N-BEATS, N-HiTS, FiLM 등은 미리 정해진 기저를 사용하기 때문에 데이터의 특성을 제대로 반영하지 못할 수 있음.
• 유연하지 못한 연결: MLP, CNN, RNN, Transformer 등은 데이터에서 기저를 학습하지만, 각 시계열과 기저 사이의 관계를 유연하게 모델링하지 못함.

BasisFormer의 제안:

• 학습 가능하고 해석 가능한 기저: 데이터에 적합한 기저를 스스로 학습하고, 그 의미를 해석할 수 있도록 함.
• 적응형 자기 지도 학습: 과거와 미래 데이터를 활용하여 기저를 학습하는 새로운 방법을 제시.
• 유연한 연결: Coef 모듈을 통해 각 시계열과 기저 사이의 유사성을 측정하여 예측에 활용.

핵심 구성 요소:

1. 적응형 자기 지도 학습: Contrastive Learning을 사용하여 과거와 미래 데이터를 기반으로 기저를 학습.
2. Coef 모듈: Bidirectional Cross-Attention을 통해 시계열과 기저 사이의 유사도를 계산.
3. Forecast 모듈: 계산된 유사도를 기반으로 미래 예측에 필요한 기저를 선택하고 결합.

기대 효과:

• 향상된 예측 성능: 데이터에 최적화된 기저를 사용하여 더 정확한 예측 결과를 얻을 수 있음.
• 높은 해석 가능성: 학습된 기저를 분석하여 시계열 데이터의 특징을 더 잘 이해할 수 있음.

 

 

 

2 Related works

 

시계열 예측 모델: 최근 딥 러닝 방법은 시계열 예측을 위한 주요 기술로 부상했습니다. 서론에서 설명했듯이 이러한 딥 러닝 방법은 일반적으로 미래 예측을 용이하게 하기 위해 기저를 사용합니다. 네트워크에서 사용되는 기저의 유형에 따라 예측 모델은 두 가지 범주로 나뉩니다. 고전적인 직교 기저를 사용하는 모델과 학습 가능한 기저를 사용하는 모델입니다. 첫 번째 그룹에는 N-BEATS, N-HiTS 및 FiLM이 포함됩니다. N-BEATS와 N-HiTS는 일반적으로 Fourier 기저를 활용한 다음 이 기저에 대한 계수를 재귀 네트워크에서 학습하여 기저가 시계열의 과거 부분을 여러 구성 요소로 분해하고 이러한 구성 요소를 추가로 집계하여 미래를 예측하는 데 도움이 되도록 합니다. FiLM은 Legendre 다항식 기저를 통해 과거 부분을 근사하고 Fourier 기저를 사용하여 노이즈를 제거합니다. 이러한 방법 그룹의 주요 단점은 기저가 미리 정의되어 있다는 것입니다. 따라서 어떤 유형의 기저를 선택할지 (예: Fourier 또는 Legendre 다항식) 그리고 기저에서 어떤 벡터를 선택할지 (예: Fourier 기저에서 어떤 주파수 구성 요소를 선택할지)에 대한 문제가 발생합니다. 반면에 Dlinear, TCN, Deepar, LogTrans, Informer, AutoFormer, FedFormer 등과 같이 학습 가능한 기저를 기반으로 하는 모델은 학습 가능한 선형 또는 컨볼루션 레이어 또는 공변량 임베딩을 기저로 사용합니다. 이러한 기저는 시계열에 적응할 수 있지만 기저와 시계열 간의 관계는 모든 시계열에 대해 고정되어 있습니다. 예를 들어, 공변량 임베딩은 각 시계열의 고유한 주파수와 주기적 패턴을 고려하지 않고 동일한 방식으로 다른 시계열의 임베딩에 추가되거나 연결됩니다. 본 논문에서는 더 정확한 예측을 위해 학습 가능한 기저와 기저와 각 시계열 간의 유연한 상관 관계를 모두 허용하는 방법을 제안합니다.

 

시계열 분석을 위한 기저 학습: 시계열 예측 외에도 학습 가능한 기저는 시계열 분류와 같은 다른 시계열 관련 작업에도 활용되었습니다. 기저 학습은 시계열의 표현 학습과 다릅니다. 전자는 공통 기저를 사용하여 시계열 세트의 패턴을 포착하는 것을 목표로 하는 반면 후자는 개별 시계열에서 특징을 추출하는 것을 목표로 합니다. 또한 기저는 Dlinear 및 TCN에서와 같이 시계열에서 특징을 추출하는 데 도움이 될 수 있습니다. 전통적으로 Fourier 및 wavelet 기저와 같이 학습 불가능한 기저가 사용됩니다. 그러나 이러한 한계를 극복하고 학습 가능한 기저를 사용할 수 있도록 하는 몇 가지 연구가 있습니다. 학습 가능한 그룹 변환은 wavelet 변환의 필터 뱅크를 일반화하고 모 wavelet에서 비선형 변환을 허용하여 시계열에서 특징을 더 잘 추출할 수 있는 유연한 필터 뱅크를 얻습니다. 이러한 방향을 따라 Balestriero et al.은 해석 가능한 매개변수가 거의 없는 Wigner-Ville 변환에 대해 학습 가능한 Gaussian 필터를 제안하고 결과 필터 뱅크가 Fourier, wavelet 및 chirplet 기저를 포함한 고전적인 필터 뱅크 사이를 보간할 수 있음을 증명합니다. 오디오 신호 처리를 위한 유사한 연구도 제안되었으며, 이는 학습 가능한 기저가 고정 기저보다 더 효과적인 특징 추출기임을 시사합니다. 따라서 본 연구에서는 학습 가능한 기저를 활용하고 시계열 예측에 대한 유용성을 입증합니다. DEPTS는 심층 확장 학습 프레임워크를 구현하여 주기적 시계열에서 복잡한 종속성과 여러 주기성으로 인해 발생하는 문제를 해결합니다. 그러나 DEPTS에서 사용하는 복잡한 초기화 및 최적화 전략과 주기적 시퀀스에만 적용할 수 있다는 제한 사항으로 인해 더 간단하고 보편적으로 적용 가능한 기저 학습 프레임워크를 개발하게 되었습니다. 구체적으로, 자기 지도 contrastive learning을 기반으로 하는 새로운 기저 학습 방법을 제안합니다.

 

자기 지도 시계열 표현 학습: 자기 지도 표현 학습 기술을 사용하여 기저를 학습하기 때문에 이 영역의 관련 연구를 살펴볼 필요가 있습니다. 이 분야에서 널리 사용되는 방법 중 하나는 후속 미래 시계열을 양의 샘플로, 무작위 비후속 미래 시계열을 음의 샘플로 처리하여 contrastive learning을 구현하여 시계열 표현을 얻는 contrastive predictive coding (CPC)입니다. 또 다른 방법인 TS-TCC는 CPC와 유사하게 두 가지 유형의 perturbation으로 데이터를 augmentation하여 두 개의 view를 얻고 교차 view 예측 작업을 대조적으로 수행합니다. 대안으로 TS2VEC은 미래 정보를 활용하지 않고 타임스탬프 마스킹 또는 무작위 자르기를 통해 양의 샘플을 생성합니다. 이러한 모든 방법은 다양한 view에서 시계열에 대한 공통 표현을 설정하려고 합니다. 이러한 접근 방식과 달리 본 연구의 목표는 시계열과 기저 간의 관계의 일관성을 유지하는 것입니다. 즉, 과거 및 미래 view에서 시계열의 표현은 다를 수 있지만 해당 기저와의 관계는 일관성을 유지해야 합니다.

 

 

주요 내용:

• 시계열 예측 모델, 기저 학습, 자기 지도 표현 학습 분야의 관련 연구들을 요약하고, BasisFormer와의 차별성을 강조합니다.

1. 시계열 예측 모델:

• 기존 연구:
  • 고전적 기저 사용 (N-BEATS, N-HiTS, FiLM): 미리 정의된 기저 사용, 데이터 특성 반영 어려움
  • 학습 가능한 기저 사용 (Dlinear, TCN, Deepar, LogTrans, Informer, AutoFormer, FedFormer): 기저와 시계열 간의 관계가 고정적, 유연성 부족
• BasisFormer: 학습 가능한 기저와 유연한 상관 관계를 모두 허용하여 더 정확한 예측

2. 시계열 분석을 위한 기저 학습:

• 기존 연구:
  • 시계열 분류 등에 활용
  • 주로 학습 불가능한 기저 (Fourier, wavelet) 사용
  • 일부 연구에서 학습 가능한 기저 사용 (wavelet 변환, Gaussian 필터)
• BasisFormer: 학습 가능한 기저를 사용하여 시계열 예측에 적용

3. 자기 지도 시계열 표현 학습:

• 기존 연구:
  • Contrastive Predictive Coding (CPC): 미래 시계열을 이용한 contrastive learning
  • TS-TCC: 데이터 perturbation을 이용한 contrastive learning
  • TS2VEC: 타임스탬프 마스킹, 랜덤 크롭을 이용한 자기 지도 학습
  • 공통적인 시계열 표현 학습에 초점
• BasisFormer: 시계열과 기저 간의 관계 일관성 유지에 초점

BasisFormer의 차별성:

• 기존 연구들은 고정된 기저를 사용하거나, 기저와 시계열 간의 관계를 유연하게 모델링하지 못하는 한계점을 가지고 있었음.
• BasisFormer는 학습 가능한 기저와 유연한 상관 관계를 모두 허용하여 이러한 한계점을 극복하고, 더 정확한 시계열 예측을 가능하게 함.
• 자기 지도 학습을 통해 시계열과 기저 간의 관계 일관성을 유지하면서, 데이터의 특성을 더 잘 반영하는 기저를 학습.

 

3 BasisFormer

C 차원의 시계열 모음이 있다고 가정해 보겠습니다. 이는 C개의 상관된 시계열을 동시에 예측해야 함을 의미합니다. 이 세트의 각 시계열은 과거 x = (x1, · · · , xI )와 미래 y = (y1, · · · , yO)로 특징지어지며, 여기서 I와 O는 각각 입력 및 출력 시퀀스 길이에 해당합니다. 본 연구의 주요 목표는 그룹의 모든 시계열의 동작을 설명할 수 있는 기저 z를 학습하고, x가 주어졌을 때 y를 예측하는 데 이를 활용하는 것입니다. 이에 따라 z는 과거 구성 요소 zx와 미래 구성 요소 zy로 나눌 수도 있습니다. 서론에서 언급했듯이 시계열 예측에 기저를 사용하려면 세 단계가 필요합니다. 적절한 기저 학습, 각 기저 벡터에 대한 시계열의 계수 계산, 기저의 미래 부분의 가중치 집계를 기반으로 예측입니다. 제안된 BasisFormer는 이러한 세 단계를 매우 다재다능한 방식으로 용이하게 합니다. 그림 1에서 볼 수 있듯이 BasisFormer의 전체 architecture에는 세 부분이 있습니다. 1 시계열을 각 기저 벡터와 비교하여 해당 계수를 결정하는 Coef 모듈, 2 계수와 기저의 미래 섹션을 기반으로 미래를 예측하는 Forecast 모듈, 3 과거 및 미래 관점에서 기저와 시계열 간의 관계를 정렬하여 기저를 학습하는 Basis 모듈입니다. 이제 각 BasisFormer 구성 요소에 대해 자세히 설명하겠습니다.

 

그림 1: Coef 모듈, Forecast 모듈, Basis 모듈로 구성된 BasisFormer의 architecture입니다. 녹색과 파란색 선은 각각 시계열 세트와 기저 벡터의 데이터 흐름을 나타냅니다. 청록색 다이아몬드는 텐서 내적을 나타냅니다. 시계열의 미래 부분의 데이터 흐름을 나타내는 점선은 학습 중에만 포함되고 추론 중에는 제거됩니다.

 

 

 

3.1 Coef module for similarity comparison between time series and basis

Coef 모듈은 시계열 세트와 기저 벡터 세트 간의 유사성을 측정하도록 설계되었습니다. 본 연구에서는 각 세트 내에서의 관계보다는 두 세트 간의 관계에 초점을 맞추고 있기 때문에, 이러한 관계를 나타내기 위해 이분 그래프를 사용합니다. 여기서 한 세트의 노드는 시계열을 나타내고 다른 세트의 노드는 기저 벡터를 나타냅니다. 결과적으로 그래프에서 두 노드를 연결하는 에지의 강도는 두 노드 간의 유사도 계수와 동일합니다. 에지 강도를 얻으려면 그래프에서 노드의 표현이 필요합니다. 본 연구에서는 그래프 attention 네트워크와 유사하게 cross-attention을 통해 노드 표현을 학습하는 양방향 cross-attention 블록 (BCAB)을 개발하여 이를 달성합니다.

먼저, 두 입력 세트 a(i) 와 b(i) 가 주어지면 cross attention 블록 (CAB)을 다음과 같이 정의합니다.

a^ = LayerNorm(MAH(a(i), b(i), b(i)) + a(i)) 
a(i+1) = CABH(a(i), b(i)) = LayerNorm(FFN(a^) + a^)

여기서 MAH 는 쿼리가 Q = Wqa, 키가 K = Wkb, 값이 V = Wvb 로 주어지는 H개의 헤드를 가진 multihead attention을 나타냅니다. a(i) 와 b(i) 간에 정보를 상호 교환함으로써 BCAB를 다음과 같이 구성할 수 있습니다.

(a(i+1), b(i+1)) = BCABH(a(i), b(i))

여기서

a(i+1) = CABH(a(i), b(i)),  b(i+1) = CABH(b(i), a(i))

a(i+1) 및 b(i+1) 을 계산하기 위한 CABH 의 매개변수는 a(i) 에서 b(i) 로의 관계와 b(i) 에서 a(i) 로의 관계의 이질성을 포착하기 위해 다를 수 있습니다.

이에 따라 C 시계열 x ∈ R^(C×I) 와 크기 N의 기저 zx ∈ R^(N×I) 가 주어지면 BCABH 의 M개 레이어를 쌓아 해당 표현을 얻을 수 있습니다. 즉, x(M) ∈ R^(C×Dc×H) 및 z(M)_x ∈ R^(N×Dc×H) 입니다. 여기서 Dc 는 BCABH 에서 각 헤드의 hidden dimension을 나타냅니다. cross attention은 Transformer 기반 모델에서 자주 발견되는 시간에 따른 계산이 아니라 시계열과 기저 간에 계산됩니다.

또한 attention 메커니즘은 시계열과 기저 벡터 간의 유연한 연결을 허용하는 데 사용됩니다. 이러한 접근 방식을 통해 각 시계열은 가장 관련성이 높은 기저 벡터에 선택적으로 attention을 기울일 수 있으며 마찬가지로 각 기저 벡터는 가장 관련성이 높은 시계열에 선택적으로 attention을 기울일 수 있습니다.

마지막으로 Coef 모듈은 H개 헤드 각각에 대한 표현 x(M) 과 z(M)_x 의 내적으로 각 기저 벡터에 대한 각 시계열의 "계수"를 계산하여 계수 텐서 c ∈ R^(C×N×H) 를 생성합니다.

 

 

 

 

3.2 Forecast module for aggregation and future prediction

계수를 얻은 후 예측을 위해 이를 활용합니다. 먼저 기저 벡터 zy 의 미래 부분을 계수를 사용하여 선형적으로 집계할 수 있는 공간으로 투영합니다. Coef 모듈은 H개 헤드에 대한 계수를 계산하므로 zy 의 투영도 일관성을 유지하기 위해 H개 헤드를 가져야 합니다. 이를 위해 병목 현상이 있는 4계층 다층 퍼셉트론 (MLP)을 사용하여 zy ∈ R^(N×O) 를 z^_y ∈ R^(N×O) 에 매핑합니다. 그런 다음 이를 H개 헤드로 분할하고 각 헤드의 크기는 N × (O/H) 이며 z˜_y ∈ R^(N×H×(O/H)) 로 표시됩니다.

각 헤드에 대해 N 차원에 대해 z˜_y 의 계수 가중치 합을 계산하여 N개의 기저 벡터를 집계합니다. 즉,

y˜[i, h] = ∑_(j=1)^N c[i, j, h]z˜y[j, h, :] 

여기서 h ∈ {1, · · · , H} 는 헤드 인덱스를 나타내고 y˜ 의 크기는 C × H × (O/H) 입니다.

다음으로, H개 헤드를 함께 연결하고 다른 4계층 MLP를 통과시켜 헤드 간에 정보를 교환합니다. 이는 서로 다른 헤드가 입력 시퀀스의 서로 다른 측면을 포착했을 수 있으며 융합 MLP가 정보를 결합하고 전체 예측 성능을 향상시키는 데 도움이 될 수 있기 때문입니다.

위 모듈의 병목 레이어는 입력 특징을 고차원 공간으로 투영하기 전에 차원을 줄이는 데 사용됩니다. 이는 투영 작업의 계산 복잡성을 줄이고 과적합을 방지하는 데 도움이 됩니다. 또한 병목 레이어를 사용하면 모델이 입력의 압축된 표현을 학습하도록 하여 더 유익한 특징을 추출하는 데 도움이 되므로 예측 정확도가 향상됩니다.

마지막으로 평균 제곱 오차 (MSE) 손실 함수를 통해 예측값 y^ 와 실제 값 y 를 비교합니다. 즉, L_pred = MSE(y^, y) 입니다.

 

 

3.3 Basis module for basis learning

이 하위 섹션에서는 자기 지도 방식으로 데이터 기반 기저를 학습하는 방법을 제시합니다. 목표는 세 가지 필수 속성을 충족하는 기저를 얻는 것입니다.

첫째, 기저 벡터와 시계열 간의 관계는 시간이 지나도 일관성을 유지해야 합니다. 따라서 기저의 과거 부분과 시계열에서 얻은 계수를 사용하여 기저의 미래 부분을 결합하여 미래를 예측할 수 있습니다. 특히, 시계열 (x, y) 와 해당 기저 (zx, zy) 가 주어지면 시계열과 기저 간의 계수 (즉, 에지 강도)는 과거 view (x, zx) 와 미래 view (y, zy) 에서 일관성을 유지해야 합니다. 즉, 과거 view에서 주어진 시계열과 특정 기저 벡터 간의 관련성은 미래 view에서도 유지되어야 합니다. 이를 위해 (x, zx) 와 (y, zy) 를 모두 Coef 모듈에 전달하여 두 view에 대한 계수 텐서 cx 와 cy 를 각각 얻습니다. 둘 다 크기는 C × N × H 입니다. 그런 다음 각 시계열에 대해 cx 에서 각 기저 벡터에 대한 계수를 앵커 포인트로, cy 에서 해당 기저 벡터에 대한 계수를 양의 샘플로, cy 에서 나머지 기저 벡터에 대한 계수를 음의 샘플로 간주하여 contrastive learning을 수행합니다. InfoNCE 손실을 최적화하여 cx 와 cy 간의 상호 정보를 최대화합니다. 이는 다음과 같습니다.

L_align = - 1/(CN)  ∑_(i=1)^C ∑_(j=1)^N log ( exp(cx[i, j, :] ⋅ cy[i, j, :]/ϵ) / ∑_(k=1)^N exp(cx[i, j, :] ⋅ cy[i, k, :]/ϵ) )

여기서 ϵ 은 정렬 분포의 부드러움을 조정하는 데 사용되는 온도를 나타냅니다.

또한 기저가 해석 가능해야 합니다. 즉, 기저에 의해 포착된 기본 패턴에 대한 통찰력을 얻을 수 있어야 합니다. 해석 가능성을 달성하기 위해 정규화 항을 사용하여 시간 경과에 따른 부드러움을 장려합니다. 즉,

L_smooth = ||zS||_2^2

여기서 과거 및 미래 view (zx, zy) 에 대한 기저 벡터를 마지막 차원을 따라 연결하여 z 를 형성하고 부드러움 행렬 S ∈ R^((I+O)×(I+O−2)) 는 다음과 같이 표현할 수 있습니다.

S =  [ 1 -2 1 ...  ... ...  ... 1 -2 1 ]

z 에 S 를 곱하면 시간에 따른 곡률인 ∥z[:, t − 1] − 2z[:, t] + z[:, t + 1]∥_2^2 를 계산합니다. S 를 사용하면 상수와 시간의 선형 함수를 추가해도 손실이 변하지 않습니다. 따라서 위의 부드러움 손실은 전체 평균 수준의 변화와 선형 추세를 수용할 수 있습니다.

마지막으로 기저는 타임스탬프의 함수여야 합니다. 따라서 입력과 두 번째 레이어의 출력 사이에 skip connection이 있는 4계층 MLP를 개발합니다. 네트워크에 대한 입력은 과거 창의 첫 번째 시점과 관련된 정규화된 타임스탬프입니다. 데이터 세트에서 시계열의 전체 길이가 T라고 가정하면 정규화된 타임스탬프는 τ = t/T 로 정의됩니다. 여기서 t ∈ {0, · · · , T − 1} 입니다. 네트워크의 출력은 현재 시간 창에 대한 기저인 N × (I + O) 텐서입니다.

전반적으로 최적화하는 손실은 다음과 같이 표현할 수 있습니다.

L = L_pred + L_align + L_smooth

BasisFormer의 성능은 (9)의 항 앞에 있는 가중치에 강력합니다. 따라서 모든 실험에서 가중치를 1로 설정합니다. 손실 함수에서 가중치에 대한 민감도 분석은 부록 A.4에서 확인할 수 있습니다.

 

 

 

 

 

 

3. BasisFormer

BasisFormer는 시계열 데이터 예측을 위해 특별히 고안된 새로운 모델입니다. 이 모델은 데이터에서 기저를 스스로 학습하고, 각 시계열 데이터에 맞는 가중치를 적용하여 예측을 수행합니다.

3.1 Coef 모듈:

• 목표: 시계열 데이터와 기저 벡터 간의 유사도를 측정합니다.
• 방법:
  • 시계열 데이터와 기저 벡터를 노드로 가지는 이분 그래프를 구성합니다.
  • 양방향 cross-attention 블록 (BCAB)을 사용하여 노드 표현을 학습합니다.
  • 각 시계열과 기저 벡터 간의 유사도를 계수로 계산합니다.
• 핵심: cross-attention 메커니즘을 통해 시계열과 기저 벡터 간의 유연한 연결을 가능하게 합니다.

3.2 Forecast 모듈:

• 목표: Coef 모듈에서 계산된 계수를 사용하여 미래 값을 예측합니다.
• 방법:
  • 기저 벡터의 미래 부분을 계수를 사용하여 선형적으로 집계합니다.
  • 여러 헤드의 정보를 결합하기 위해 융합 MLP를 사용합니다.
  • 병목 레이어를 사용하여 계산 복잡성을 줄이고 과적합을 방지합니다.
• 핵심: 계수 가중치 합을 통해 미래 예측값을 생성합니다.

3.3 Basis 모듈:

• 목표: 데이터 기반 기저를 자기 지도 방식으로 학습합니다.
• 방법:
  • 과거 및 미래 시점의 데이터를 사용하여 contrastive learning을 수행합니다.
  • 시간 경과에 따른 기저의 부드러움을 유지하기 위해 정규화 항을 사용합니다.
  • 타임스탬프 정보를 기저에 반영합니다.
• 핵심: 데이터의 특성을 잘 반영하고 해석 가능한 기저를 학습합니다.

전반적인 흐름:

1. Coef 모듈에서 시계열 데이터와 기저 벡터 간의 유사도를 계산합니다.
2. Forecast 모듈에서 계산된 계수를 사용하여 미래 값을 예측합니다.
3. Basis 모듈에서 자기 지도 학습을 통해 데이터에 적합한 기저를 학습합니다.

 

 

 

 

 

 

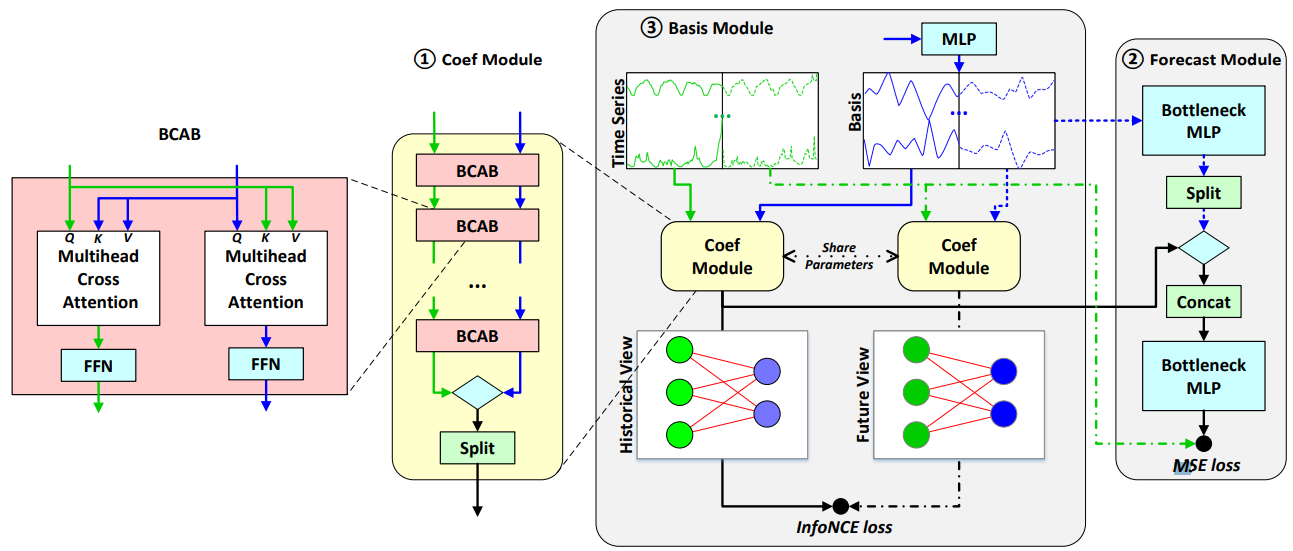
1. 입력:

• 녹색 노드: 시계열 데이터 (과거 x, 미래 y) ➡️ Coef 모듈로 입력됩니다.
• 파란색 노드: 기저 벡터 (과거 zx, 미래 zy) ➡️ Basis 모듈에서 생성됩니다.

2. Coef 모듈:

• 과거 시계열 데이터 (x) 와 과거 기저 벡터 (zx) 를 사용하여 유사도 계수를 계산합니다.
• BCAB (Bidirectional Cross-Attention Block) 을 통해 시계열과 기저 벡터 간의 관계를 학습합니다.
  • 멀티헤드 cross attention: 시계열과 기저 벡터 사이의 다양한 관계를 파악합니다.
  • FFN (Feed-Forward Network): 학습된 정보를 비선형적으로 변환합니다.
• 계산된 유사도 계수는 빨간색 에지로 표현됩니다.
• 과거 데이터 (x, zx) 와 미래 데이터 (y, zy) 에 대해 각각 Coef 모듈을 적용하여 두 개의 유사도 계수 세트를 얻습니다.

3. Basis 모듈:

• Coef 모듈에서 얻은 두 개의 유사도 계수 세트를 사용하여 기저 벡터를 학습합니다.
• InfoNCE loss: 과거와 미래 시점에서 시계열과 기저 벡터 간의 관계가 일관되도록 학습합니다.
• 시간 정보를 반영하고, 기저 벡터가 부드럽게 변화하도록 학습합니다.
• 학습된 기저 벡터 (zx, zy) 는 Coef 모듈과 Forecast 모듈에 사용됩니다.

4. Forecast 모듈:

• Coef 모듈에서 계산된 유사도 계수와 기저 벡터의 미래 부분 (zy) 을 사용하여 미래 값을 예측합니다.
• MLP (Multi-Layer Perceptron): 기저 벡터를 변환하고, 여러 헤드의 정보를 결합합니다.
• Bottleneck layer: 계산 복잡성을 줄이고 과적합을 방지합니다.
• 예측 결과는 실제 값과 비교하여 MSE loss를 계산합니다.

5. 학습:

• BasisFormer는 Coef 모듈, Forecast 모듈, Basis 모듈을 end-to-end 방식으로 학습합니다.
• 즉, 전체 모델을 하나의 네트워크로 구성하고, 모든 모듈을 동시에 학습합니다.
• 학습 과정에서 InfoNCE loss와 MSE loss를 최소화하는 방향으로 모델을 업데이트합니다.

요약:

BasisFormer는 시계열 데이터와 기저 벡터를 입력으로 받아, Coef 모듈에서 유사도 계수를 계산하고, Forecast 모듈에서 미래 값을 예측합니다. Basis 모듈은 자기 지도 학습을 통해 데이터에 적합한 기저를 학습합니다. 전체 모델은 end-to-end 방식으로 학습되어 최적의 성능을 달성합니다.

 

 

 

1. 초기 단계: 학습이 안 된 기저 zx

처음엔 학습되지 않은 상태의 기저 zx와 시계열 데이터 x가 Coef 모듈에 들어가. 여기서 Coef 모듈은 x와 임의의 기저 zx 사이의 유사도 계수 c를 계산해. 이 유사도는 각 시계열 데이터가 해당 기저와 얼마나 관련이 있는지를 나타내.

1. Forecast 모듈: 유사도 계수로 미래 기저 zy 결합

Coef 모듈에서 얻은 유사도 계수 c를 이용해, Forecast 모듈에서는 미래에 해당하는 기저 zy를 예측해. 유사도 계수 c와 미래 기저 zy를 가중합(weighted sum) 방식으로 결합해 예측된 미래 값 y^를 생성해.

1. Basis 모듈: 기저 zx와 zy 학습

시계열 데이터를 넣어 학습하는 과정에서, Basis 모듈은 시계열 데이터의 과거와 미래에 해당하는 기저 zx와 zy를 학습해. 이때, Basis 모듈은 시계열 데이터의 과거 x와 미래 y 간의 일관성을 유지하면서 기저를 학습하는데, 이는 대조 학습(contrastive learning)을 통해 이루어져. 과거 시계열과 미래 시계열이 동일한 패턴을 공유하도록 만드는 거야.

1. 반복되는 학습 과정: 기저의 점진적 업데이트

초기에는 기저가 학습되지 않았지만, 모델이 여러 번의 반복 학습을 거치면서 zx와 zy는 점점 더 정확한 기저 패턴으로 학습돼. 시계열 데이터가 반복적으로 입력되고, 매번 Coef 모듈과 Forecast 모듈을 통해 유사도 계수가 계산되고 기저 zy가 가중합으로 결합되면서, Basis 모듈에서 기저가 점진적으로 학습돼. 즉, 학습 과정 동안 기저는 계속해서 업데이트되며, zx와 zy는 시계열 데이터의 패턴을 더 잘 반영하게 돼.

1. 최종 상태: 학습이 완료된 기저와 정확한 예측

학습이 충분히 이루어지면, zx와 zy는 시계열 데이터의 고유한 주기와 패턴을 잘 반영하는 기저로 학습돼. Coef 모듈과 Forecast 모듈에서 이 학습된 기저를 사용해, 정확한 미래 예측을 할 수 있게 되는 거지.

 

 

 

 

 

질문1 : 학습 초기의 zx와 zy가 랜덤하거나 잘못된 패턴을 가지게끔 들어가면 학습에서 이상한 구간으로 발산할 수 있을 것 같은데 어떻게 해결했는지.

 

질문2 zx와 zy가 비슷하게끔 loss가 짜여진 것 같은데 그게 과연 좋은 원하는 기저인지 어떻게 타당하게 판단하는지?

 

질문3 기저와 각 시게열 간의 유연한 관계를 학습하지 못한다고 비판했는데 저자들의 basisformer를 보면 최종아웃풋은 y햇이고 유사도 계수 c를 활용하긴 했지만 그게 정말 잘 학습이 된건지 의문이다.