LLM : 논문리뷰 : AlphaZero-Like Tree-Search can Guide Large Language Model Decoding and Training

AlphaZero-Like Tree-Search 논문 정리 노트

Purpose of the Paper (논문의 목적)

기존 연구인 Tree-of-Thought (ToT) 와 Reasoning via Planning (RAP) 은 Large Language Models (LLMs) 의 reasoning 능력을 향상시키기 위해 tree-search 알고리즘을 활용했지만, 다음과 같은 근본적인 한계를 가졌습니다.

1. 얕은 search depth: 최대 depth 가 10 또는 7 로 제한되어, long-horizon planning 이 필요한 복잡한 문제에 적용하기 어려웠습니다. AlphaZero 가 chess 나 Go 에서 깊은 search depth 를 보여준 것에 비해 미흡했습니다.
2. Prompt 기반 value function 의 의존성: GPT-4 와 같은 advanced LLM 의 prompt 를 통해 value function 을 얻었기 때문에, prompt 디자인에 민감하고 general applicability 가 부족했습니다. Prompt 기반 self-evaluation 은 항상 reliable 하지 않다는 문제점도 존재했습니다.

본 논문의 목적은 이러한 기존 tree-search 방법들의 한계를 극복하고, LLMs 의 decoding 과 training 모두를 효과적으로 guide 할 수 있는 AlphaZero 와 유사한 tree-search learning framework (TS-LLM) 을 제시하는 것입니다. 특히, learned value function 을 활용하여 다양한 task, model size, search depth 에 adaptable 하고 scalable 한 framework 를 구축하고자 했습니다.

Key Contributions (핵심 기여)

본 논문의 핵심 기여는 다음과 같이 요약할 수 있습니다.

1. TS-LLM Framework 제안: AlphaZero-like deep tree-search 와 learned LLM-based value function 을 결합한 새로운 framework 인 TS-LLM (Tree-Search enhanced LLM) 을 제안했습니다. TS-LLM 은 LLM 의 inference 와 training 과정 모두를 guide 할 수 있도록 설계되었습니다.
2. General Applicability 및 Scalability: TS-LLM 은 learned value function 을 사용하기 때문에 prompt 에 대한 의존성을 줄이고, 다양한 task 와 model size 에 적용 가능합니다. 실험적으로 125M 에서 7B parameter model 까지 적용 가능함을 보였으며, GPT-3.5 와 비교해도 더 나은 evaluation 성능을 나타냈습니다. 또한, 최대 depth 64 까지 deep tree search 가 가능하여 기존 ToT, RAP 에 비해 scalability 를 크게 확장했습니다.
3. New LLM Training Paradigm 제시: Tree-search operation 을 policy improvement operator 로 간주하여, tree search 를 통해 policy 를 개선하고, distillation 과 value function learning 을 통해 policy 를 더욱 향상시키는 iterative training process 를 제시했습니다. 이는 inference decoding 을 넘어 LLM training paradigm 자체를 확장하는 새로운 시도입니다.
4. 다양한 Task 에서 Empirical Validation: reasoning, planning, alignment, decision-making task 등 다양한 task 에서 TS-LLM 의 effectiveness 를 empirical 하게 입증했습니다. 특히, Game24, GSM8k, ProntoQA, RLHF, Chess Endgame 등 다양한 search space 를 가진 task 에 대한 실험을 통해 TS-LLM 의 general versatility 를 강조했습니다.

Novelty (참신성)

본 논문의 novelty 는 다음과 같은 측면에서 찾을 수 있습니다.

1. Learned Value Function 기반 Tree-Search: 기존 ToT, RAP 과 달리 prompt 기반 self-evaluation 대신 learned LLM-based value function 을 tree-search 에 통합하여 general applicability 와 reliability 를 높였습니다. Prompt 에 대한 의존성을 줄이고 다양한 task 에 적용 가능한 scalable framework 를 구축한 점이 novel 합니다.
2. AlphaZero-like Training Framework for LLMs: AlphaZero 알고리즘의 핵심 아이디어를 LLM training 에 적용하여 iterative policy improvement 및 value function learning 을 수행하는 새로운 training paradigm 을 제시했습니다. Tree-search 를 policy improvement operator 로 활용하여 LLM 의 reasoning 능력 자체를 향상시키는 접근 방식은 기존 연구와 차별화됩니다.
3. TS-LLM 의 다양한 변형 (MCTS-a, MCTS-Rollout 등) 및 심층 분석: TS-LLM framework 내에서 다양한 tree-search 알고리즘 변형 (MCTS-a, MCTS-Rollout, BFS-V, DFS-V) 을 제안하고, 각 알고리즘의 특징과 장단점을 비교 분석했습니다. Computation cost, search space, aggregation 방법 등 다양한 요소를 심층적으로 분석하여 TS-LLM framework 의 효과를 다각도로 검증했습니다.

Experimental Highlights (실험 결과 하이라이트)

실험 결과에서 주목할 만한 점은 다음과 같습니다.

1. Learned Value Function 의 효과: Game24, GSM8k task 에서 prompt-based value function (GPT-3.5, LLaMA-2B ToT) 보다 learned value function (LLaMA-V) 을 사용했을 때 더 높은 accuracy 를 달성했습니다. 이는 learned value function 이 prompt 에 덜 의존적이고 더 reliable 함을 보여줍니다.
2. AlphaZero-like 알고리즘 (MCTS-a, MCTS-Rollout) 의 우수성: RLHF, Chess Endgame task 와 같이 long-horizon planning 이 중요한 task 에서 MCTS-a, MCTS-Rollout 이 BFS-V, DFS-V, CoT-Greedy baseline 보다 significantly 더 나은 성능을 보였습니다. 얕은 tree search 에서는 baseline 과 comparable 한 accuracy 를 유지하면서, 깊은 tree search 가 필요한 task 에서 강점을 드러냈습니다.
3. Computation Cost 와 Performance Trade-off: Path@1 metric 에서는 TS-LLM 이 CoT-Greedy 보다 더 많은 computation cost 를 소모하지만, Equal-Token setting 에서 비교했을 때 CoT-SCORM 과 comparable 하거나 더 나은 성능을 보였습니다. TS-LLM 이 computation cost 대비 효과적인 성능 향상을 제공

 

 

 

 

Abstract

최근 Tree-of-Thought (ToT) 및 Reasoning via Planning (RAP)와 같은 연구는 tree-search algorithms을 사용하여 multi-step reasoning을 안내함으로써 LLMs의 reasoning 능력을 향상시키는 것을 목표로 합니다. 이러한 방법은 pre-trained model을 value function으로 사용하도록 prompting하고 낮은 search depth를 가진 문제에 중점을 둡니다. 결과적으로, 이러한 방법은 pre-trained LLM이 효과적인 value function 역할을 할 수 있는 충분한 지식이 없는 도메인이나 long-horizon planning이 필요한 도메인에서는 작동하지 않습니다.

이러한 한계를 해결하기 위해, 우리는 LLMs를 위한 AlphaZero와 유사한 tree-search learning framework (TS-LLM)를 제시하며, learned value function을 사용한 tree-search가 LLM decoding을 어떻게 안내할 수 있는지 체계적으로 보여줍니다. TS-LLM은 두 가지 주요한 방식으로 차별화됩니다.

(1) learned value function과 AlphaZero와 유사한 algorithms을 활용하여, 우리의 접근 방식은 광범위한 tasks, 모든 크기의 language models, 다양한 search depths를 가진 tasks에 일반적으로 적용될 수 있습니다.
(2) 우리의 접근 방식은 inference와 training 모두에서 LLMs를 안내하여 LLM을 반복적으로 개선할 수 있습니다.

reasoning, planning, alignment, decision-making tasks 전반에 걸친 실험 결과는 TS-LLM이 기존 접근 방식을 능가하고 depth가 64인 trees를 처리할 수 있음을 보여줍니다.

 

 

 

 

 

 

1. Introduction

LLMs (OpenAI, 2023; Touvron et al., 2023a)는 광범위한 natural language tasks에서 그 잠재력을 입증했습니다. 최근의 수많은 연구는 더 크고 더 높은 품질의 일반 또는 특정 도메인 data의 curation (Touvron et al., 2023a; Zhou et al., 2023; Gunasekar et al., 2023; Feng et al., 2023; Taylor et al., 2022), 더 정교한 prompt design (Wei et al., 2022; Zhou et al., 2022; Creswell et al., 2022), 또는 Supervised Learning 또는 Reinforcement Learning (RL)을 사용한 더 나은 training algorithms (Dong et al., 2023; Gulcehre et al., 2023; Rafailov et al., 2023)을 포함하여 LLMs의 task 해결 능력을 향상시키는 데 집중했습니다.

RL로 LLMs를 training 할 때, LLMs의 generation은 자연스럽게 Markov Decision Process (MDP)로 공식화될 수 있고 특정 objectives로 최적화될 수 있습니다. 이 공식을 따라, ChatGPT (Ouyang et al., 2022)는 RL from Human Feedback (RLHF) (Christiano et al., 2017)을 활용하여 human preference에 맞게 LLMs를 최적화하는 주목할 만한 성공 사례로 부상했습니다.

LLMs는 tree search와 같은 planning algorithms을 통해 더욱 안내될 수 있습니다. 이 분야의 예비 연구에는 depth/breadth-first search를 사용한 Tree-of-Thought (ToT) (Yao et al., 2023; Long, 2023)와 MCTS를 사용한 Reasoning-via-Planing (RAP) (Hao et al., 2023)가 포함됩니다. 그들은 self-evaluation을 통해 LLM에 의해 확장된 trees에서 searching하는 성능 향상을 성공적으로 입증했습니다.

이러한 발전에도 불구하고, 현재 방법에는 뚜렷한 한계가 있습니다.

첫째, tree-search algorithms의 value functions은 LLMs를 prompting하여 얻습니다. 결과적으로, 이러한 algorithms은 일반적인 적용 가능성이 부족하고 잘 설계된 prompts와 고급 LLMs의 강력한 기능에 크게 의존합니다. model requirements 외에도, 우리는 또한 섹션 4.2.1에서 이러한 prompt-based self-evaluation이 항상 신뢰할 수 있는 것은 아니라는 것을 보여줄 것입니다.

둘째, ToT와 RAP는 tree search를 위해 BFS/DFS와 MCTS를 사용하여 상대적으로 단순하고 얕은 tasks에 그 능력을 제한합니다. 그들은 최대 depth가 10 또는 7로 제한되어 있는데, 이는 chess나 Go에서 AlphaZero가 달성한 depth보다 훨씬 작습니다 (Silver et al., 2017). 결과적으로, ToT와 RAP는 큰 analytical depths와 장기 planning horizons을 요구하는 복잡한 문제로 어려움을 겪을 수 있으며, 확장성을 감소시킵니다.

이러한 문제를 해결하기 위해, 우리는 tree-search enhanced LLM (TS-LLM)을 소개합니다. 이는 tree-search를 활용하여 일반적인 natural language tasks에서 LLMs의 성능을 향상시키는 AlphaZero와 유사한 framework입니다. TS-LLM은 learned LLM-based value function을 사용한 AlphaZero와 유사한 deep tree-search로 이전 작업을 확장하여 inference와 training 모두에서 LLM을 안내할 수 있습니다. 이전 작업과 비교하여 TS-LLM은 다음과 같은 두 가지 새로운 기능을 제공합니다.

• TS-LLM은 일반적으로 적용 가능하고 확장 가능한 pipeline을 제공합니다.
  • 일반적으로 적용 가능합니다: learned value function을 통해 TS-LLM은 다양한 tasks와 모든 크기의 LLMs에 적용될 수 있습니다. 우리의 learned value function은 prompt-based 대응보다 더 신뢰할 수 있고 잘 설계된 prompts나 고급, 대규모 LLMs를 필요로 하지 않습니다. 우리의 실험은 TS-LLM이 125M에서 7B parameters에 이르는 LLMs에 대해 작동할 수 있고 GPT-3.5와 비교해도 더 나은 evaluation을 제공한다는 것을 보여줍니다.
  • TS-LLM은 또한 확장 가능합니다: TS-LLM은 deep tree search를 수행하여 LLM generation을 위한 tree-search를 최대 64의 depth까지 확장할 수 있습니다. 이는 ToT의 10과 RAP의 7을 훨씬 뛰어넘습니다.
• TS-LLM은 inference decoding을 넘어 새로운 LLM training paradigm으로 잠재적으로 사용될 수 있습니다. tree-search operation을 policy improvement operator로 취급함으로써, 우리는 tree search를 통해 policy를 개선하고 tree search trajectories의 ground-truth training labels을 통해 value function을 개선하는 반복적인 프로세스를 수행할 수 있습니다.

reasoning, planning, alignment, decision-making tasks에 대한 포괄적인 실증적 평가를 통해, 우리는 TS-LLM의 핵심 설계 요소에 대한 심층 분석을 제시하고, 다양한 변형의 기능, 장점, 한계를 탐구합니다. 이는 TS-LLM이 LLM decoding 및 training을 안내하는 보편적인 framework로서의 잠재력을 보여줍니다.

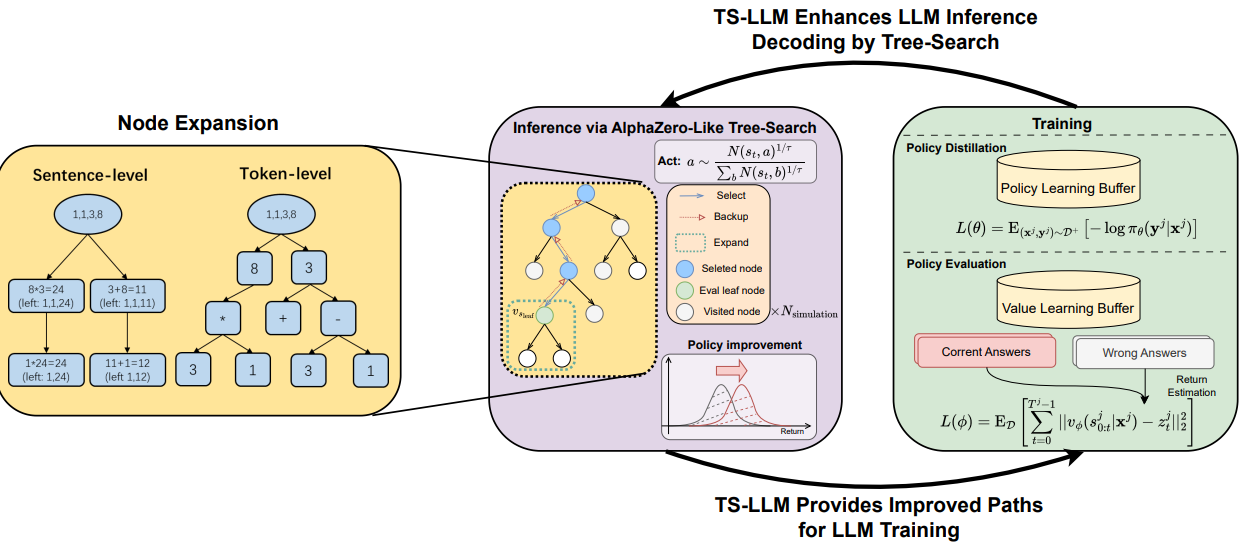
Figure 1:

(a) 왼쪽: Game24에서의 두 가지 node expansion paradigms: sentence-level과 token-level. 이 task에서는 sentence-level 설정을 채택합니다.

(b) 오른쪽: TS-LLM은 tree-search와 training에 대한 반복적인 프로세스로 구성됩니다. 먼저, TS-LLM은 tree-search를 통해 LLM inference를 향상시켜 개선된 trajectories를 얻고, training set을 보강합니다. LLM은 보강된 training set에 대해 policy distillation과 value function learning (policy evaluation)을 수행하여 개선되도록 추가로 trained 될 수 있습니다.

 

 

 

1. Introduction 정리 노트 (AI 연구자 대상)

이 논문의 핵심:

기존 LLMs 연구는 data, prompt engineering, training algorithms 개선에 집중했지만, 이 논문은 tree-search를 활용하여 LLMs의 reasoning 능력을 향상시키는 새로운 framework인 TS-LLM을 제안합니다. 특히, learned value function을 기반으로 한 AlphaZero와 유사한 deep tree-search를 통해 기존 방법의 한계를 극복하고, LLMs를 inference뿐만 아니라 training 단계에서도 guidance를 제공합니다.

기존 연구(ToT, RAP)의 한계:

• Prompting에 의존하는 value function: 일반화가 어렵고, 고성능 LLMs 및 정교한 prompt에 의존적입니다. 또한, prompt-based self-evaluation은 신뢰성이 떨어집니다.
• 얕은 search depth: BFS/DFS, MCTS 사용으로 인해 최대 depth가 10 또는 7로 제한되어 복잡한 문제 해결에 한계가 있습니다.

TS-LLM의 차별점:

1. 일반화 및 확장성:
   • Learned value function: 다양한 task 및 크기의 LLMs에 적용 가능하며, GPT-3.5보다 우수한 evaluation을 제공합니다.
   • Deep tree-search: 최대 depth 64까지 확장하여 복잡한 문제 해결 능력을 향상시킵니다.
2. 새로운 LLM training paradigm:
   • Tree-search를 policy improvement operator로 활용하여, policy와 value function을 반복적으로 개선합니다.

요약:

TS-LLM은 learned value function을 사용한 deep tree-search를 통해 기존 LLMs 연구의 한계를 극복하고, 더욱 일반적이고 확장 가능한 LLM guidance framework를 제안합니다. 또한, inference뿐만 아니라 training 단계에서도 LLMs를 개선할 수 있는 새로운 paradigm을 제시합니다.

 

2. Related Work

Multistep Reasoning in LLMs

Language models에서의 multistep reasoning은 base model을 개선하는 것(Chung et al., 2022; Fu et al., 2023; Lewkowycz et al., 2022)부터 LLMs를 단계별로 prompting 하는 것(Kojima et al., 2022; Wei et al., 2022; Wang et al., 2022; Zhou et al., 2022)에 이르기까지 광범위하게 연구되었습니다.

또한, learned reward models (Uesato et al., 2022; Lightman et al., 2023) 및 self-evaluation (Shinn et al., 2023; Madaan et al., 2023)을 포함한 evaluations을 통한 reasoning을 향상시키는 데 중점을 둔 보다 관련성이 높은 일련의 연구가 있습니다. 이 연구에서 우리는 multistep decision-making process 설정 하에 value function과 reward model을 learning하여 multistep reasoning tasks와 token-level RLHF alignment tasks에 evaluations을 적용합니다.

Search-Guided Reasoning in LLMs

대부분의 CoT 접근 방식이 linear reasoning structure를 사용했지만, 최근에는 trees와 같은 non-linear reasoning structures를 조사하기 위한 노력이 이루어졌습니다(Jung et al., 2022; Zhu et al., 2023). 더 최근에는 더 나은 reasoning paths를 찾기 위해 trees에서 searching하기 위한 다양한 접근 방식이 적용되었습니다. 예를 들어, Xie et al. (2023)의 beam search, Yao et al. (2023)의 depth-/breadth-first search, (Hao et al., 2023)의 Monte-Carlo Tree Search가 있습니다.

이러한 방법과 비교하여, TS-LLM은 learned value function을 사용한 tree search guided LLM decoding 및 training framework로, reasoning tasks와 RLHF alignment tasks와 같은 다른 시나리오 모두에 더 일반적으로 적용할 수 있습니다. 공간의 제약으로 인해 포괄적인 비교는 부록 A에 남겨 둡니다.

Finetuning LLMs with Augmentation

최근에는 augmented data를 사용하여 LLMs를 개선하기 위한 노력도 이루어졌습니다. Rejection sampling은 multistep reasoning (Yuan et al., 2023a; Zelikman et al., 2022) 및 human preference와의 alignment (Dong et al., 2023; Bai et al., 2022)와 같은 단일/다중 task(s)에 대한 LLMs의 능력을 향상시키기 위한 finetuning data augmentation을 위한 간단하고 효과적인 접근 방식입니다.

augmented dataset이 주어지면, reinforcement learning 접근 방식도 LLMs를 finetune하는 데 사용되었습니다(Gulcehre et al., 2023; Luo et al., 2023). 이전 연구와 비교하여 TS-LLM은 tree search를 policy improvement operator로 활용하여 LLMs와 value function을 모두 training하기 위한 augmented samples를 generate합니다.

 

 

 

2. Related Work 정리 노트 (AI 연구자 대상)

핵심 키워드: Multistep Reasoning, Search-Guided Reasoning, Finetuning with Augmentation

이 논문과 관련된 연구 분야:

1. LLMs에서의 Multistep Reasoning:
   • Base model 개선 및 prompting 기법 연구
   • Evaluations을 통한 reasoning 향상: learned reward models, self-evaluation
   • 이 논문의 차별점: multistep decision-making process 하에서 value function과 reward model을 learning하여 multistep reasoning 및 token-level RLHF alignment에 evaluations 적용
2. LLMs에서의 Search-Guided Reasoning:
   • Non-linear reasoning structures (e.g., trees) 탐구:
   • Tree search를 통한 reasoning paths 탐색: beam search, depth-/breadth-first search, Monte-Carlo Tree Search
   • 이 논문의 차별점: learned value function을 활용한 tree search guided LLM decoding 및 training framework를 제안하며, reasoning tasks와 RLHF alignment tasks에 모두 적용 가능
3. Augmentation을 통한 LLMs Finetuning:
   • Rejection sampling: data augmentation을 위한 간단하고 효과적인 기법
   • Reinforcement learning: augmented dataset을 활용한 LLMs finetuning
   • 이 논문의 차별점: tree search를 policy improvement operator로 활용하여 LLMs와 value function을 모두 training하기 위한 augmented samples 생성

요약:

이 논문은 기존의 multistep reasoning, search-guided reasoning, augmentation을 통한 finetuning 연구들을 기반으로, learned value function을 활용한 tree search framework를 제안합니다. 특히, multistep decision-making process에서의 value function learning, tree search를 통한 decoding 및 training, policy improvement operator로서의 tree search 활용 등이 이 논문의 핵심적인 차별점입니다.

이 정리 노트가 AI 연구자들이 논문의 핵심을 빠르게 파악하는 데 도움이 되기를 바랍니다.

 

 

3. Enhancing LLMs with Tree Search

이 섹션에서는 LLMs decoding과 training을 guide하는 다재다능한 tree-search framework인 TS-LLM을 제안합니다. 우리는 그 핵심 구성 요소에 대한 체계적이고 포괄적인 분석을 수행합니다. TS-LLM은 그림 1에 요약되어 있습니다.

3.1. Problem Formulation

우리는 language generation process를 multistep Markov Decision Process (MDP)로 공식화합니다. natural language tasks의 특수성은 action과 state가 모두 language space에 있다는 것입니다. LLMs는 tokens의 sequences를 actions으로 sampling하는 policy πθ 역할을 할 수 있습니다.

output sequence의 길이를 T, input prompt의 길이를 L이라고 가정할 때, LLM policy가 prompt (input prefix) x = (x0, x1, ..., xL−1)가 주어졌을 때 output sequence y = (y0, y1, ..., yT −1)를 생성할 확률은 다음과 같습니다.

πθ(y|x) = Π (t=0 to T-1) πθ(yt|x0:L−1, y0:t−1)

주어진 natural language task에 대해, 우리는 timestep t에서의 intermediate generation yt에 대한 task performance feedback으로 reward function R(yt|x0:L−1, y0:t−1)을 정의할 수 있습니다. 일반적인 tasks에 대한 대규모 및 고품질 intermediate reward labels이 부족하기 때문에, 일반적으로 첫 번째 T-1 timestep의 모든 intermediate reward가 0이고 마지막 T번째 step만 0이 아닌 sparse reward 설정입니다. 일반적인 사례는 RLHF alignment task일 수 있으며, LLM은 전체 generation을 완료한 후에 reward signal을 받을 수 있습니다.

같은 논리에 따라, y는 또한 sentences의 sequence로 볼 수 있습니다. 위의 문제 공식을 고려할 때, 우리는 더 나은 generation 문제를 더 높은 cumulative reward를 위한 최적화로 성공적으로 전환합니다. 이 논문에서는 tree-search algorithms을 사용하여 이를 최적화하는 방법에 중점을 둡니다.

특정 natural language task는 일반적으로 state space (language 사용)와 reward function (task objective/metrics 사용)을 미리 정의합니다. 남은 것은 action space의 정의, 즉 tree-search algorithm의 맥락에서 action node의 정의입니다. tree search algorithms은 discrete action space (Silver et al., 2017; Schrittwieser et al., 2020a) 및 continuous action space (Hubert et al., 2021)를 포함하여 전통적인 RL 연구에서 다양한 action spaces에 대한 효율성을 입증했습니다.

LLMs에 대한 tree-search의 경우, 그림 1의 왼쪽에 표시된 것처럼 다음과 같은 두 가지 action space 설계를 고려합니다.

• Sentence-level action nodes: step/sentence-level structure(예: chain-of-thought reasoning)를 가진 tasks의 경우, 각 thought를 sentence-level action node로 취급하는 것이 자연스럽습니다. 이것은 또한 ToT (Yao et al., 2023)와 RAP (Hao et al., 2023)에서 채택된 기술입니다. 각 non-terminal node에 대해, search tree는 몇 가지 가능한 후속 intermediate steps를 sampling하고 중복된 generations을 삭제하여 확장됩니다.
• Token-level action nodes: discrete action space MDP에서의 tree-search와 유사하게, 우리는 각 token을 LLM policy에 대한 discrete action으로 취급할 수 있으며 tree search는 token-level에서 수행될 수 있습니다. intermediate steps가 명시적으로 정의되지 않은 tasks(예: RLHF)의 경우, output sequence를 tokens로 분할하는 것이 좋은 선택일 수 있습니다.

일반적으로 search space는 algorithm에 구애받지 않는 두 가지 parameters, 즉 tree의 최대 너비 w와 tree의 최대 깊이 d에 의해 결정됩니다. LLM generation에서 두 action space 설계는 search space에 대한 장단점이 있습니다.

generation을 sentences로 분할함으로써, sentence-level action nodes는 상대적으로 얕은 tree(낮은 tree 최대 깊이)를 제공하여 tree-search process를 단순화합니다. 그러나 sentence-level generation의 큰 sample space는 모든 가능한 sentences의 완전한 열거를 불가능하게 만듭니다. 우리는 Sampled MuZero (Hubert et al., 2021)의 idea와 유사하게 expansion 중에 w개의 nodes를 subsample하기 위해 최대 tree 너비 w를 설정해야 합니다(node는 확장되면 고정됨). 이러한 subsampling은 tree-search space와 LLM generation space 사이의 w에 의해 결정되는 차이를 초래합니다.

token-level action nodes의 경우, search space 불일치와 추가 계산 부담을 없앨 수 있지만, tree의 depth를 크게 늘려 tree-search를 더 어렵게 만듭니다.

3.2. Guiding LLM Inference Decoding with Tree Search

tree-search algorithms의 이점 중 하나는 gradient 계산이나 update 없이 단순한 search만으로 cumulative reward를 최적화할 수 있다는 것입니다. 이 섹션에서는 고정된 LLM policy가 주어졌을 때, tree search approaches로 LLM inference decoding을 guide하는 방법을 설명하는 전체 pipeline을 제시합니다.

3.2.1. LEARNING AN LLM-BASED VALUE FUNCTION

tree-search algorithms의 경우, 신뢰할 수 있는 value function v와 reward model rˆ을 구성하는 방법이 주요 문제입니다. ToT와 RAP는 GPT-4 또는 LLaMA-33B와 같은 고급 LLMs를 prompting하여 이 두 models를 얻습니다. tree search algorithm을 일반적으로 적용할 수 있도록 하기 위해, 우리의 방법은 state s에 조건부로 learned LLM-based value function vϕ(s)와 learned final-step outcome reward model (ORM) rˆϕ를 활용합니다.

대부분의 tasks가 sparse-reward problems (Uesato et al., 2022)로 공식화될 수 있기 때문입니다. 우리는 주로 language-based tasks를 다루기 때문에, shared value network와 reward model을 활용합니다. 이 구조는 input tokens의 각 위치에 scalar를 출력하는 MLP가 있는 decoder-only transformer입니다. 그리고 일반적으로 LLM value의 decoder는 원래 LLM policy πθ의 decoder에서 조정되거나, LLM value vϕ와 policy πθ가 decoder를 공유할 수 있습니다(Silver et al., 2017).

sentence-level로 확장된 intermediate step st의 경우, 마지막 token의 prediction scalar를 value prediction vϕ(st)로 사용합니다. final reward는 전체 sentences (x0:L−1, y0:T −1)를 model에 입력할 때 마지막 token에서 얻을 수 있습니다.

따라서, 우리는 language model πθ를 policy로 사용하여 task training dataset을 사용하여 generations을 sample합니다. training data의 true label 또는 주어진 reward function을 사용하여 크기가 |Dtrain|인 sampled tuple Dtrain = {(x j , y j , rj )}j 집합을 얻을 수 있습니다. 여기서 x j 는 input text, y j = s j 0:Tj−1 는 T j steps의 output text이고 r j = R(y j |x j )는 ground-truth reward입니다.

대부분의 RL algorithms의 critic training과 유사하게, 우리는 각 단일 step t에 대해 TD-λ (Sutton, 1988) 또는 MC 추정(Sutton & Barto, 2018)으로 value target z j t 를 구성합니다. value network는 mean squared error에 의해 최적화됩니다.

L(ϕ) = ED [ Σ (t=0 to Tj-1) ||vϕ(s j 0:t |x j ) − z j t ||^2_2 ] (1)

ORM rˆϕ(y0:T −1|x0:L−1)은 동일한 objective로 learned 됩니다. 정확한 value function과 ORM을 training하는 것은 tree-search process에 주요 guidance를 제공하기 때문에 매우 중요합니다. 우리는 실험 섹션에서 신뢰할 수 있는 value function과 ORM을 learning하는 방법을 더 자세히 설명합니다.

3.2.2. TREE SEARCH ALGORITHMS

learned value function이 주어지면, 이 섹션에서는 다섯 가지 유형의 tree-search algorithms을 제시합니다. 자세한 배경, 예비 정보 및 비교는 부록 C.1에 남겨 둡니다.

• Value Function-Based Tree-Pruning을 사용한 Breadth-First 및 Depth-First Search (BFS-V/DFS-V): 이 두 search algorithms은 ToT (Yao et al., 2023)에서 채택되었습니다. 핵심 idea는 효율적인 search를 위해 value function을 사용하여 tree를 prune하는 것이지만, 이러한 pruning은 tree의 너비 또는 깊이에서 각각 발생합니다. BFS-V는 cumulative reward를 objective로 하는 beam-search로 간주될 수 있습니다.
• MCTS: 이 접근 방식은 RAP (Hao et al., 2023)에서 채택되었으며, 고전적인 MCTS(Kocsis & Szepesvari ´ , 2006)를 참조합니다. terminal nodes의 value를 back-propagates하고 value의 Monte-Carlo 추정에 의존하며 initial state node에서 searching을 시작합니다.

ToT와 RAP에서 채택한 이러한 algorithms 외에도, 우리는 AlphaZero와 유사한 tree-search의 두 가지 새로운 변형을 고려합니다.

• Value Function Approximation을 사용한 MCTS (MCTS-α): 이것은 AlphaZero (Silver et al., 2017)에서 활용된 MCTS 변형입니다. initial state에서 시작하여 state st의 node를 root node로 선택하고 select, expand and evaluate, backup으로 구성된 여러 번의 search simulations을 수행합니다. 여기서 learned value function에 의해 evaluated된 leaf node value는 모든 조상 nodes로 backpropagated됩니다. search 후, 우리는 root node의 지수화된 방문 횟수에 비례하는 action을 선택합니다. 즉, a ∼ N(st,a) 1/τ / Σb N(st,b) 1/τ 이고 해당 다음 state로 이동합니다. 위의 반복은 완료될 때까지 반복됩니다.

MCTS-α는 두 가지 주요 기능이 있습니다.

      *   첫째, MCTS-α는 action을 취하면 이전 states로 되돌아갈 수 없습니다. 따라서 섹션 3.2.3에서 논의할 여러 search가 수행되지 않는 한 initial state에서 search를 다시 시작할 수 없습니다.
*   둘째, MCTS와 달리 MCTS-α는 value function을 활용하므로 Monte-Carlo 추정을 얻기 위해 전체 generation을 완료할 필요 없이 intermediate steps 동안 backward operation을 수행할 수 있습니다.
    

content_copy download

Use code with caution.

• MCTS-Rollout: MCTS와 MCTS-α의 기능을 결합하여, 우리는 tree search를 위한 새로운 변형 MCTS-Rollout을 제안합니다. MCTS와 유사하게 MCTS-Rollout은 항상 initial state node에서 시작합니다. MCTS-α와 유사하게 search simulations을 추가로 수행하고, backup process는 value function을 사용하여 intermediate step에서 발생할 수 있습니다. process가 N개의 완전한 answers를 찾거나 계산 제한(예: 최대 tokens 수)에 도달할 때까지 위의 operations을 반복합니다. MCTS-Rollout은 MCTS-α의 offline version으로 볼 수 있으므로 유사한 적용 범위를 가질 수 있습니다. 유일한 차이점은 MCTS-Rollout이 항상 처음부터 search를 다시 수행하기 때문에 더 나은 성능을 위해 token consumption을 확장할 수 있다는 것입니다.

3.2.3. MULTIPLE SEARCH AND SEARCH AGGREGATION

Wang et al. (2022)과 Uesato et al. (2022)에서 영감을 받아 LLM이 여러 번 sampling하고 candidates를 aggregating하여 reasoning tasks에 대한 성능을 향상시킬 수 있다는 점에 착안하여, TS-LLM은 또한 multiple tree searches 또는 one search에서 multiple generations(BFS beam size > 1 설정)에 의해 생성된 N개의 완전한 answers를 aggregate할 가능성이 있습니다.

multiple tree searches를 수행할 때, 우리는 일반적으로 intra-tree search 설정을 채택합니다. Intra-tree search는 동일한 tree에서 multiple tree searches를 수행하므로 state space는 정확히 동일합니다. 이러한 방법은 search tree를 여러 번 재사용할 수 있으므로 계산적으로 효율적입니다. 그러나 이전 tree search가 이후 tree searches에 영향을 줄 수 있기 때문에 multiple generations의 다양성이 감소할 수 있습니다. 또한, search space는 sentence-level action space에서 제한됩니다. 왜냐하면 그들은 multiple tree searches에 걸쳐 확장되면 고정되기 때문입니다.

우리는 expansion process에서 resampling을 허용하는 Inter-tree Search라는 대안 설정을 위해 부록 E.7을 참조하고, 추가 사양 없이 우리 논문의 모든 설정은 intra-tree search 설정 하에 있습니다.

다음 단계는 이러한 search results를 aggregate하여 final answer를 얻는 것입니다. learned ORM을 사용하여 다음과 같은 세 가지 aggregation 방법을 고려합니다.

• Majority-Vote: Wang et al. (2022)은 majority vote를 사용하여 answers를 aggregate합니다. f
  * = arg maxf Σyj 1final ans(yj )=f , 여기서 1은 indicator function입니다.
• ORM-Max: outcome reward model이 주어지면, aggregation은 최대 final reward를 가진 answer f를 선택할 수 있습니다. f
  * = final ans(arg maxyj rˆϕ(y j |x j )).
• ORM-Vote: outcome reward model이 주어지면, aggregation은 reward의 합으로 answer f를 선택할 수 있습니다. 즉, f
  * = arg maxf Σyj ;final ans(yj )=f rˆϕ(y j |x j )입니다.

3.3. Enhancing LLM Training with Tree Search

섹션 3.2에서는 tree-search가 inference time 동안 LLM의 decoding process를 guide하는 방법에 대해 논의합니다. 이러한 guidance는 더 나은 decoding strategy로 이어지고 주어진 tasks의 성능을 향상시킵니다. 즉, tree-search guidance는 policy improvement operator 역할을 할 수 있습니다. 이를 바탕으로 우리는 새로운 training 및 finetuning paradigm을 제안합니다.

초기 LLM policy πθold (원래 training set에 대해 supervised finetuning을 수행하여 trained 됨)와 초기 LLM value 및 ORM: vϕold , rˆϕold (원래 training questions를 sampling하여 식 1로 trained 됨)이 있다고 가정하면, 다음과 같은 반복적인 process를 가질 수 있습니다.

• Policy Improvement: πθold , vϕold , rˆϕold 를 기반으로 training set에 대해 tree-search를 수행하여 개선된 generations을 얻고, 결과적으로 augmented dataset D와 filtered positive examples D+를 얻습니다.
• Policy Distillation: tree-search로 개선된 dataset D+를 사용하여, tree-search positive trajectories를 모방함으로써 LLM policy는 supervised loss를 통해 πθnew로 더 개선될 수 있습니다.

L(θ) = E(xj ,yj )∼D+ [− log πθ(y j |x j )] (2)

• Policy Evaluation: augumented dataset D에 대해 식 1의 loss로 value function vϕnew 와 ORM rˆϕnew 를 train합니다.

이 세 가지 process는 LLM을 반복적으로 refine하기 위해 주기적으로 수행될 수 있습니다. 이러한 반복적인 process는 generalized policy iteration (Sutton & Barto, 2018)에 속하며, AlphaZero의 training에도 사용되는 절차입니다. 우리의 경우, training process는 tree-search augmented dataset에서 세 가지 networks를 finetuning하는 것을 포함합니다.

(1) Policy network πθ: trajectories의 tokens을 target으로 하는 cross-entropy loss 사용

(2) Value network vϕ: trajectories의 temporal difference (TD) 또는 Monte-Carlo (MC) 기반 value estimation을 target으로 하는 Mean squared error loss 사용

(3) ORM rˆϕ: trajectories의 final reward를 target으로 하는 Mean squared error loss 사용

3.4. Tree Search’s Extra Computation Burdens

tree-search algorithms은 특히 legal child nodes와 해당 value를 계산하기 위한 node expansion 단계에서 필연적으로 추가 계산 부담을 가져옵니다. ToT 및 RAP와 같은 이전 방법론은 동일한 수의 generation paths (Path@N)를 사용하여 baseline algorithms에 대해 성능을 benchmark하는 경향이 있습니다. 이 접근 방식은 tree-search process의 추가 계산 요구 사항을 간과합니다. 우리는 또한 계산 효율성과 엔지니어링 과제에 대한 토론을 위해 독자들에게 부록 D.3을 참조하도록 합니다.

보다 공정한 비교를 위해서는 node expansion을 위해 생성된 tokens 수를 모니터링해야 합니다. 이를 통해 유사한 token generation 조건에서 작동할 때 algorithms의 성능을 합리적으로 비교할 수 있습니다. 우리는 실험에서 이 문제를 다룹니다(섹션 4.2.2).

 

 

3. Enhancing LLMs with Tree Search 정리 노트 (AI 연구자 대상)

핵심: Tree-Search를 활용하여 LLMs의 decoding과 training을 향상시키는 framework, TS-LLM 제안

3.1 Problem Formulation:

• Language generation을 multistep MDP로 공식화: action과 state가 모두 language space
• Sparse reward setting: 대부분의 경우, 마지막 step을 제외하고 intermediate reward는 0
• 목표: Tree-Search를 통해 cumulative reward를 최대화하는 최적화 문제로 변환
• Action space 정의 (Tree-Search의 action node):
  • Sentence-level: chain-of-thought reasoning과 같이 step/sentence 구조를 가진 task에 적합, tree depth는 얕지만, sample space가 커서 subsampling 필요 (trade-off 존재)
  • Token-level: RLHF와 같이 intermediate step이 명시되지 않은 task에 적합, search space 불일치는 없지만, tree depth가 깊어짐

3.2 Guiding LLM Inference Decoding with Tree Search:

• 핵심: Tree-Search를 통해 inference 단계에서 cumulative reward를 최적화
• 3.2.1 Learning an LLM-based Value Function:
  • Learned value function (vϕ) 및 final-step outcome reward model (ORM, rˆϕ) 활용: GPT-4, LLaMA-33B prompting 대신
  • Shared value network & reward model: decoder-only transformer + MLP (scalar 출력)
  • Training: TD-λ 또는 MC estimation을 사용한 value target 구성 및 MSE loss로 최적화
• 3.2.2 Tree Search Algorithms:
  • 기존: BFS-V/DFS-V (ToT), MCTS (RAP)
  • 새로운 제안:
    • MCTS-α: AlphaZero에서 사용된 MCTS 변형, intermediate step에서 value function을 사용한 backpropagation 가능
    • MCTS-Rollout: MCTS와 MCTS-α를 결합, initial state에서 시작하여 MCTS-α와 유사하게 search simulation 수행, offline version으로 token consumption 확장 가능
• 3.2.3 Multiple Search and Search Aggregation:
  • Multiple tree search: intra-tree search (동일 tree) 또는 inter-tree search (resampling 허용)
  • Aggregation 방법: Majority-Vote, ORM-Max, ORM-Vote

3.3 Enhancing LLM Training with Tree Search:

• 핵심: Tree-Search를 policy improvement operator로 활용하여 LLM training
• 반복적인 process:
  1. Policy Improvement: Tree-Search로 augmented dataset D 및 positive examples D+ 생성
  2. Policy Distillation: D+를 사용한 supervised learning으로 policy πθ 개선 (imitation learning)
  3. Policy Evaluation: D를 사용하여 value function vϕ와 ORM rˆϕ training
• Generalized policy iteration (AlphaZero training과 유사): Tree-Search augmented dataset에서 policy network, value network, ORM을 finetuning

3.4 Tree Search’s Extra Computation Burdens:

• Node expansion 단계에서 추가 계산 발생
• 공정한 비교를 위해: Node expansion을 위해 생성된 tokens 수 모니터링

이 논문만의 핵심:

• Learned value function과 ORM을 활용한 tree-search framework: 일반화 가능성 향상
• MCTS-α와 MCTS-Rollout 제안: AlphaZero와 유사한 tree-search의 새로운 변형
• Tree-Search를 policy improvement operator로 활용: LLM training에 tree-search를 통합한 새로운 paradigm 제시
• Tree-Search의 computation burden을 고려한 성능 평가: 공정한 비교를 위한 새로운 기준 제시

이 정리 노트가 AI 연구자들이 논문의 핵심을 빠르게 파악하는 데 도움이 되기를 바랍니다.