정보량과 엔트로피의 의미 (정보이론의 시작)
먼저 정보이론에 대해서 설명하겠습니다.

정보이론의 아버지라고 불리는 클로드 섀넌이 정립한 이론입니다.
정보이론(Information theory)은 정보의 양과 통신에서의 정보 전송량 등을 측정하고, 처리하는 수학적인 이론입니다.
정보이론에서 가장 기본적인 개념은 정보량(Information)입니다. 정보량은 어떤 사건이 얼마나 놀라운가에 따라서 결정됩니다. 즉, 더 드문 사건일수록 정보량이 크며, 반대로 더 일어날 가능성이 높은 사건일수록 정보량이 작아집니다. 정보량을 수학적으로 나타낼 때는 엔트로피(Entropy)라는 개념을 사용합니다.
예를들면 로또에 당첨되지 않았어~ 라는 말은 굉장히 흔한 일이기 때문에 정보량이 굉장히 작습니다.
하지만 로또에 당첨되었다는 것은 굉장히 흔하지 않은 일이기 때문에 정보량이 많은 것입니다.
정보이론에서는 또한 정보를 압축하는 방법에 대해서도 다루는데, 이를 위해 코드(Code)라는 개념이 사용됩니다. 코드란 어떤 정보를 다른 형태로 변환하는 것을 말하며, 정보의 압축을 위해서는 더 짧은 코드를 사용해야 합니다.
정보이론은 통신 분야에서도 많이 활용됩니다. 예를 들어, 어떤 데이터를 전송할 때는 그 데이터의 정보량을 줄이기 위해 압축을 하거나, 전송 중에 손실이 생기는 경우에는 에러 검출 및 수정을 위한 코드를 사용합니다.
또한, 정보이론은 머신러닝 분야에서도 활용되며, 특히 결정트리(Decision Tree) 알고리즘에서 엔트로피를 사용하여 정보량을 계산하고, 분류(Classification)나 회귀(Regression) 문제를 해결하는 데에 사용됩니다.
엔트로피
앞서 정보량에대해서 서술하였습니다. 엔트로피는 정보량과 매우 관련있습니다.
정보이론에서 엔트로피(Entropy)란 어떤 정보의 불확실성, 혼돈도를 나타내는 척도입니다. 정보의 엔트로피가 높을수록, 즉 정보의 불확실성이 높을수록 정보량이 많아지게 됩니다.
즉 정보량이 많다 = 희귀한 사건이다
희귀한 사건일수록 불확실성이 높아지게 됩니다.
희귀한사건 = 정보량이 높다 = 불확실성이 높다.
정보이론에서는 엔트로피를 다음과 같은 식으로 계산합니다.
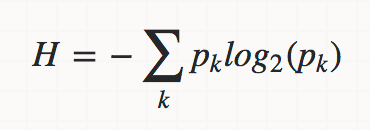
여기서 H(X)는 확률 변수 X의 엔트로피를 나타내며, p(x)는 X가 어떤 값을 가질 확률을 나타냅니다. log2는 밑이 2인 로그 함수를 나타냅니다.
위 식에서 보면, 엔트로피는 X의 확률 분포에 따라 달라지며, 각각의 값에 대한 정보량을 구한 뒤 이를 가중 평균한 것입니다. 즉, 엔트로피가 높다는 것은 X가 가질 수 있는 값들이 그 확률 분포상으로 고르게 분포되어 있어서, 그 값이 어떤 것일지 예측하기 어렵다는 것을 의미합니다.
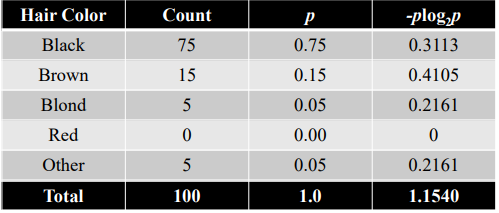
엔트로피는 결정트리(Decision Tree) 알고리즘에서 중요하게 사용되며, 각 분기점에서의 정보량을 계산하여 데이터를 분할하는 데에 사용됩니다. 엔트로피를 최대한 줄이는 방향으로 분기점을 선택하면, 좀 더 명확한 결정을 내릴 수 있게 됩니다.