Central Limit Theorem 이란?

 

 

중심극한정리:

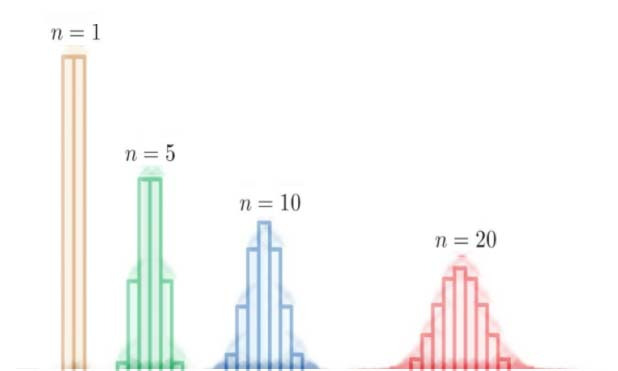
• 표본의 크기가 충분히 크면, 모집단의 분포 모양과 상관없이 표본 평균들의 분포는 정규분포에 가까워진다.

의미:

• 다양한 현상을 정규분포로 모델링 가능: 많은 자연 현상이나 사회 현상은 여러 요인들의 복합적인 작용으로 나타나는데, 이러한 현상들은 중심극한정리에 의해 정규분포로 근사하여 분석할 수 있습니다. 덕분에 통계적 추론이나 예측 등 다양한 분야에 정규분포를 활용할 수 있습니다.

 

 

주의사항:

• 표본의 크기: 표본의 크기가 충분히 커야 중심극한정리가 적용됩니다. 일반적으로 표본의 크기가 30 이상이면 충분하다고 간주하지만, 모집단의 분포 형태에 따라 필요한 표본 크기는 달라질 수 있습니다.

예시:

• 전 국민의 키: 각 개인의 키는 다양한 유전적, 환경적 요인의 영향을 받지만, 충분히 많은 사람들의 키를 표본으로 추출하여 평균을 내면 그 평균들의 분포는 정규분포에 가까워집니다.
• 주사위 던지기: 한 번 던졌을 때 나오는 눈의 수는 균등분포를 따르지만, 여러 번 던져서 나온 눈의 수의 평균을 구하는 행위를 여러 번 반복하면, 그 평균들의 분포는 정규분포에 가까워집니다.

중심극한정리는 통계학에서 매우 중요한 개념이며, 다양한 분야에서 널리 활용되고 있습니다.